A magassága a háromszög
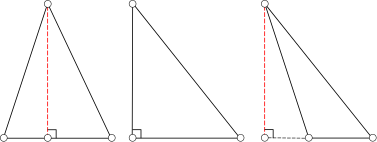
A magassága a háromszög különböző típusú
A magassága a háromszög - a merőleges. csökkent a tetején a háromszög, hogy az ellentétes oldalon (pontosabban, a vonalon, amely tartalmazza a szemközti oldalon). Attól függően, hogy a magassága a háromszög típusú belül lehetnek a háromszög (a hegyesszögű háromszög) egybeesik az oldalán (amely a láb egy derékszögű háromszög), vagy hely, kívül a háromszög a tompaszögű háromszög.
Tulajdonságok A metszéspontok a három magasságban a háromszög (orthocenter)
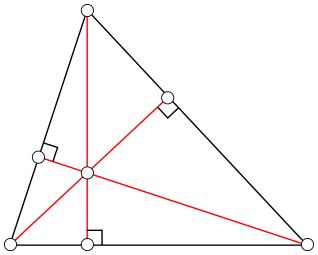
(A személyazonosság igazolása kell használni képletek
Mint metszéspontja E kellene két háromszög magasságát.)
- Az utóbbi állítás is következménye tételek pedál háromszög csúcsai (előre és hátra) [1]
- Orthocenter isogonally konjugátum közepén a körülírt kör.
- Orthocenter fekszik ugyanabban a sorban a súlypontja. A központ a körülírt kör és a kör közepén kilenc pontot (lásd. Euler vonal).
- Orthocenter akut háromszög közepén beírható kör ő ortotreugolnik.
- A központ köré írt kör egy háromszög orthocenter a háromszög csúcsai a felezőpontja az oldalán a háromszög. Az utolsó háromszög nevezzük háromszög hozzáadjuk az első háromszög.
- Az utóbbi tulajdonság alapján megállapítható, mint: A központ köré írt kör a háromszög a orthocenter háromszög tovább.
- Pont szimmetrikus háromszög orthocenter körüli oldalán fekszenek a körülírt.
- Point szimmetrikus orthocenter háromszög felezőpontja az oldalán, is alapul a körülírt kör és egybeesik a pont átmérősen ellentett megfelelő csúcsait.
- Ha a G - leírt ΔABC központja körhöz, O H → = O A → + O B → + O C →> => +> + >>.
- | O H | 9 R = 2 - (a 2 + b 2 + c 2) - (a ^ ^ + b + c ^) >>>. ahol R - a kör sugara; a. b. c - a hossza az oldalán a háromszög.
- A távolság orthocenter háromszög csúcsa, hogy kétszer a távolság a központtól a körülírt kör, hogy az ellenkező oldalon.
- Bármely részes levonni orthocenter a kereszteződés a körülírt kör mindig többszöröse az Euler kör a felére. Orthocenter központja homothety a két kört.
- Hamilton-tétel. Három vonalszakaszok összekötő orthocenter egy hegyesszögű háromszög, melynek csúcsai osszuk három háromszög azonos Euler kör (kör kilenc pont), az eredeti hegyesszögű háromszög.
- Vizsgálat Hamilton-tétel.
- Három vonalszakaszok csúcsokat összekötő a orthocenter az akut háromszög, osszuk három Hamilton háromszög. amelynek egyenlő sugarú körök leírt.
- A sugarak a körök által leírt Hamilton három háromszög egyenlő a kör sugara körülírt a kezdeti hegyesszögű háromszög.
- A hegyesszögű háromszög, orthocenter fekszik háromszög belsejében; tompaszöget - egy háromszög; Egy jobb -, hogy a tetején a derékszög.
Tulajdonságok egy egyenlő szárú háromszög magasságát
- Ha a kettő megegyezik a magassága a háromszög, a háromszög - egyenlő szárú (Steiner-tétel - Lemus), a harmadik pedig a magassága mind a medián és a felezővonal a szög, amelyből származik.
- Ezzel szemben, a két magasság egyenlő, egyenlő oldalú háromszögben, a harmadik pedig a magassága mind a medián és a felezővonal.
- Az egyenlő oldalú háromszögben mindhárom magasság egyenlő.
Alapvető tulajdonságait a háromszög magasságát
- magasságok bázisok alkotnak egy úgynevezett ortotreugolnik. Megvan a saját tulajdonságait.
- Ortotreugolnika le a kör - egy kör Euler. Ezen a körön is három oldalán a háromszög és a közepén a három középső három szegmens összekötő orthocenter a csúcsai a háromszög.
- Másik készítmény a legújabb funkciók:
- Euler-tétel egy kilenc pont köre. Bázisok három magasságban tetszőleges háromszög, a középső három az oldalán (alapozza belső medián) és három középső összekötő szakaszok a csúcsokat a orthocenter. minden hazugság azonos kerületen (a kerülete kilenc pont).
- Tétel. Mindenesetre háromszög, a szegmens összekötő az alapja a két magasságban a háromszög, a háromszög vág mint ezt.
- Tétel. A háromszög összekötő szakasz két alap háromszög magasságát, hogy hazugság mindkét oldalán, egy harmadik oldalon antiparalel amellyel nincs közös pontjuk. Annak két végén, valamint a két csúcsot, amely a harmadik fél mindig lehetséges, hogy dolgozzon ki egy kört.
További ingatlanok a háromszög magasságát
- Ha a háromszög sokoldalú (egyenlő szárú), a belső felezővonal. Az elvégzett bármely csomóponttól között fekszik a belső és a medián végzett ugyanabból vertex magassága.
- Triangle Magasság isogonally konjugátum átmérője (sugár) a körülírt kör. levonni a két csúcsot.
- Egy hegyesszögű háromszög, magassága két hasonló háromszögek levágták róla.
- A magassága a derékszögű háromszög. levonni a csúcsa a derékszög. felosztja két háromszög hasonló az eredetihez.
Tulajdonságok legkisebb magassága a háromszög
A legkisebb magassága a háromszög számos extrém tulajdonságai. Például:
- Minimum merőleges vetülete egy háromszög a vonalak síkjában fekvő háromszög hossza megegyezik az alsó a magassága.
- Minimum egyenes szakasz egy repülőgép, amelyen keresztül húzhatja hajlíthatatlan háromszög alakú lemez kell hossza megegyezik az alsó, a magasból a lemez.
- A folyamatos mozgás a két pont a kerülete a háromszög egymás felé, a maximális távolság közöttük a mozgás során az első és a második találkozón nem lehet kevesebb, mint a hossza a legkisebb háromszög magasságát.
- A legkisebb magassága a háromszög mindig átmegy a belsejében a háromszög.
Tétel a magassága egy derékszögű háromszög
Ha a magassága egy téglalap alakú ABC háromszög, a hossza h. Az elvégzett a csúcsa a derékszög osztja a átfogója hossz C a hossz m és n. megfelelő befogó b és egy. akkor a következő egyenletek igazak:
A tétel a nyúlványok