Szinusz, koszinusz, tangens és kotangens a trigonometria

Ebben a cikkben bemutatjuk, hogyan kell biztosítani meghatározások szinusz, koszinusz, tangens és kotangensét a szög és a számot trigonometria. Itt beszélünk a jelölést, akkor példákat rekordok, hogy ad egy grafikus ábrázolása. Végül párhuzamot fogalma közötti szinusz, koszinusz, tangens és kotangens a geometria és a trigonometria.

Oldalnavigáció.

Meghatározása szinusz, koszinusz, tangens és kotangens

Egy hegyesszög egy derékszögű háromszög

Természetesen ismert geometriájú meghatározó szinusz, koszinusz, tangens és kotangens hegyesszög egy derékszögű háromszög. Ezek arányként az oldalán egy derékszögű háromszög. Íme a vallomását.

Sine a hegyesszögben egy derékszögű háromszög - az aránya a másik lábát a átfogója.

Kotangensét hegyesszögben egy derékszögű háromszög - az arány a szomszédos oldalsó, hogy egy ellentétes.

Van még bevezetni jelölést szinusz, koszinusz, tangens és kotangens - bűn. cos. és tg ctg volt.

Például, ha az ABC - derékszögű háromszög a derékszögű C szinusz a hegyesszög egyenlő az arány a másik lábát a átfogója BC AB. azaz sin∠A = BC / AB.

Ezek a definíciók lehetővé teszik, hogy értékeit számítjuk szinusz, koszinusz, tangens és kotangens hegyesszöget az ismert derékszögű háromszög oldalhosszúságú és az ismert értékek szinusz, koszinusz, tangens, kotangens, és a hossza az egyik fél, hogy megtalálják a hosszát a másik oldalról. Például, ha tudjuk, hogy a befogó AC derékszögű háromszög átfogója és az egyenlő 3. 7. AB egyenlő tudtuk számítani a koszinusza hegyesszög A definíció szerint: cos∠A = AC / AB = 3/7.

forgásszög

A trigonometria szöget elkezd keresni szélesebb körben - a koncepció az elforgatás szögét. Nagysága a forgásszög, szemben a hegyesszögben nem korlátozódik a körét 0 és 90 fok, az elfordulás szögét fokban (radiánban) fejezhető bármely kívánt valós szám -∞ és + ∞.

Ennek fényében, mivel a meghatározás szinusz, koszinusz, tangens és kotangens nem hegyesszög, és az a szög bármely nagyságú - az elforgatás szögét. Ezek adott x és y koordinátákat A1 pont. amelybe az úgynevezett kezdeti pont (1, 0), miután annak forgási szöggel α pont körül O - kezdődő Descartes-féle derékszögű koordináta-rendszer és a központ az egység kör.

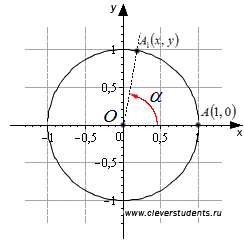
Sine a forgásszög α - az ordináta a pont A1. azaz sinα = y.

Kotangensét a forgásszög α az aránya az abszcissza A1 pont annak ordináta, azaz ctgα = x / y.

A szinusz és koszinusz meghatározzuk minden szög α. mert mindig meg tudja állapítani az abszcissza és ordináta a pont, amelyet úgy kapunk, forgatásával a kezdeti pontban olyan szögben α. A tangens és kotangens nincsenek definiálva bármilyen szögben. Tangens nincs meghatározva ezek a szögek α. amelyben a kiindulási pont mozog, hogy a pontot az abszcissza a nulla (0, 1) vagy (0, -1). és ez történik szögek 90 ° + 180 ° · k. k∈Z (π / 2 + π · k rad). Valóban, ezek az elfordulási szögek expressziós tga = y / x értelmetlen, mert van egy nullával osztani. Ami a kotangensét, hogy nincs definiálva ilyen szögek α. amelyben a kiindulási pont mozog, hogy egy pont nulla ordináta (1, 0) vagy (-1, 0). mint ahogy az a szög a 180 ° · k. k∈Z (π · k rad).

Így a szinusz és koszinusz függvényeket definiálja minden elfordulási szögek, tangens meghatározható minden szög kivételével 90 ° + 180 ° · k. k∈Z (π / 2 + π · k rad), és a kotangensét - az összes szögek, kivéve 180 ° · k. k∈Z (π · k rad).

A fogalommeghatározások már ismert számunkra utal bűn. cos. és tg ctg. használják őket jelölésére a szinusz, koszinusz, tangens és kotangens elfordulási szög (néha megtalálható tan jelölést és gyermekágy. felelős tangens és kotangens). Mivel a szinusz az elfordulási szög 30 fok felírható sin30 °. bejegyzések tg (-24 ° 17 „), és az érintő ctgα Meet forgási szög -24 fok 17 perc és a kotangensét a forgásszög α. Emlékezzünk vissza, hogy a szög szimbólum „rad” gyakran kihagyják radiánban felvétel közben. Például, a koszinusza a forgásszög három pi rad általában jelöljük cos3 · π.

A rész lezárásához érdemes megjegyezni, hogy a beszélgetés a szinusz, koszinusz, tangens és kotangensét a forgásszög gyakran kihagyják az „viszont a sarokban”, vagy a „forgatás”. Vagyis ahelyett, hogy a kifejezés „sine alfa forgásszög” általában arra használják a kifejezést „sine a szög alfa” vagy még rövidebb - „sinus alfa”. Ugyanez vonatkozik a koszinusz és tangens és kotangens.

Továbbá, mondjuk, hogy a definíciók a szinusz, koszinusz, tangens és kotangens hegyesszög egy derékszögű háromszög összhangban vannak az adatok meghatározása csak szinusz, koszinusz, tangens és kotangens forgásszög értéke 0-90 fok. Ez magyarázza azt az utolsó bekezdésben ezt a cikket.

Következő szükség van, hogy megszabaduljon a sarkok és így a meghatározása szinusz, koszinusz, tangens és kotangens szám helyett a szöget.

Szinusz, koszinusz, tangens, kotangens, és t a száma egyenlő szinusz, koszinusz, tangens és a kotangensét a forgásszög radiánban t ill.

Például a koszinusza 8 · π definíciója szerint egy szám egyenlő a koszinusza szög 8 · π rad. A koszinusza szög 8 · π rad egyenlő egysége, így a koszinusza 8 · π értéke 1.

Van egy másik megközelítés meghatározása A szinusz, koszinusz, tangens és kotangens számát. Ez abban áll, hogy minden egyes valós szám t rendelünk egy pontot a készülék kör középpontja a derékszögű koordináta-rendszert, és a szinusz, koszinusz, tangens, kotangens, és meghatározott keresztül koordinátáit ezen a ponton. Vizsgáljuk meg ezt részletesebben.

Megmutatjuk, hogyan lehet beállítani a levelezést a valós számok és a pontokat a kör:

• 0 van rendelve egy kiindulási pont Egy (1, 0);
• pozitív szám t rendelünk egy pontot a készülék kör, amely azt fogja kapni, ha mozgunk egy kört a kiindulási pont ellentétes irányban, és menj át az út hossza t;
• negatív egész t rendelt egy pontot a készülék kör, amely azt fogja kapni, ha mozgunk egy kört a kiindulási pont az óramutató járásával megegyező irányba, és megy át az út hossza | t |.

Most megyünk a meghatározások a szinusz, koszinusz, tangens és kotangensét t. Tegyük fel, hogy a számot t megfelelő pont köre A1 (x, y) (például, a száma pi / 2; A1 megfelel a pont (0, 1)).

Sine hívott szám t ordináta pontján az egység kör számának megfelelő t. azaz sint = y.

Koszinusz t abszcissza pont az úgynevezett egység kör számának megfelelő t. azaz költsége = x.

T érintő az aránya az ordináta, hogy az abszcissza a pont az egység kör számának megfelelő t. azaz, TGT = y / x. Egy másik ekvivalens készítmény, a tangensét t - ez az arány a szinusz a koszinusza ez a szám, azaz, TGT = sint / költség.

Kotangensét abszcissza az aránya t, hogy az ordináta az egység kör számának megfelelő t. azaz, ctgt = x / y. Egy másik készítmény az alábbiak szerint: tangense t - az aránya t koszinusz, hogy a szinusz t. ctgt = költség / sint.

Itt megjegyezzük, hogy csak azokat az adatokat a meghatározás összhangban van a meghatározás elején ezt a bekezdést. Sőt, a lényeg az egység kör számának megfelelő t. Ez egybeesik azzal a ponttal eredő forgása kezdőpont egy szöget radiánban t.

A másik az, hogy tisztázza ezt a pontot. Mondjuk, van egy rekord sin3. Honnan tudod, hogy a sinus 3 vagy sinus elfordulási szöge radiánban 3 kérdés? Általában kiderül a szövegkörnyezetből, különben valószínűleg nem alapvető érték.

Trigonometrikus függvények Sarki és numerikus argumentum

Meghatározások szerint az előző bekezdésben, az egyes forgásszög α felel meg határozott értéket sinα. mivel a cos érték. Továbbá, az összes a forgási szög 90 ° -tól különböző + 180 ° · k. k∈Z (π / 2 + π · k rad) értékeknek felel meg tg. de más, 180 ° · k. k∈Z (π · k rad) - értékek ctgα. Ezért sinα. cosa. és tga ctgα - függvénye a szög α. Más szóval - ez a funkció a szögletes érv.

Ugyanígy beszélhetünk a funkciók szinusz, koszinusz, tangens és kotangensét száma érvelés. Tény, hogy minden valós szám t felel meghatározott érték sint. valamint a költség. Ezen kívül minden szám kivételével π / 2 + π · k. k∈Z értékeknek felel meg a TGT. és a szám tc · k. k∈Z - értékek ctgt.

A funkciók szinusz, koszinusz, tangens és kotangens úgynevezett alap trigonometrikus függvények.

A szövegkörnyezetből általában egyértelmű, trigonometrikus függvények szögletes érv vagy numerikus argumentum van dolgunk. Ellenkező esetben, akkor feltételezhetjük, hogy a független változó az intézkedés a szög (szögletes érv) és egy numerikus érv.

Ugyanakkor az iskola elsősorban tanult numerikus függvények, azaz funkciók, amelyek érveket a megfelelő függvény értékei azok a számok. Ezért, ha beszélünk funkciók, célszerű figyelembe venni a trigonometrikus függvények működik numerikus érveket.

Kommunikációs meghatározásai geometria és trigonometria

Ha figyelembe vesszük a szög α értéke 0 és 90 fok, akkor az adatokat a keretében trigonometria meghatározására szinusz, koszinusz, tangens és a kotangensét a forgásszög teljes mértékben összhangban vannak a meghatározások szinusz, koszinusz, tangens és kotangens hegyesszög egy derékszögű háromszög, amelyek során a geometria. Lássuk be azt.

Ábrázolják egy Descartes-féle derékszögű koordináta-rendszer Oxy egység kör. Megjegyzés: a kezdőpont A (1, 0). Forgatás keresztül szögben α értéke 0 és 90 fok, megkapjuk az A1 pont (x, y). Csökkenés a pont A1 a Ox tengelyen merőleges A1 H.

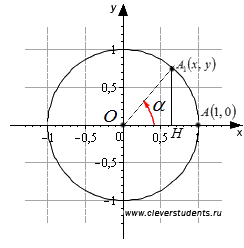
Könnyen belátható, hogy a derékszögű háromszög A1 OH szög egyenlő a forgásszög α. hossza szomszédos a sarokban a láb OH egyenlő az abszcisszán pont A1. azaz, | OH | = x. a hossza a másik lábát, hogy a szög A1 H A1 egyenlő az ordináta ponton. azaz, | A1 H | = y. OA1 és a hossza a átfogója egyenlő eggyel, mivel ez egy egység kör sugara. Ezután, a meghatározás a geometria a szinusz hegyesszög α egy derékszögű háromszög egyenlő A1 OH ellentétes kapcsolatban átfogója lábát, azaz sinα = | A1 H | / | OA1 | = y / 1 = y. És definíció trigonometrikus szinusz szögelfordulás α egyenlő az ordináta a pont A1. azaz sinα = y. Ez azt mutatja, hogy a meghatározás a szinusz hegyesszög a derékszögű háromszög egyenértékű meghatározására a szinusz a forgásszög α a α a 0 és 90 fok.

Hasonlóképpen, az egyik tudja mutatni, hogy meghatározása a koszinusz, tangens és kotangens hegyesszög α összhangban áll a definíciók koszinusz, tangens és kotangens forgásszög α.