Másodfokú függvény 2

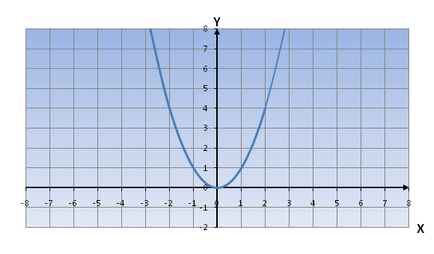
Parabola két részből áll: az egyik tárolja a negyedek I, ahol a pozitív értékek az X és Y, és a második rész - II negyedekbe, ahol a negatív értékek X és Y jelentése a pozitív értékek.

Ha megy az egyik ága a parabola származó -∞ és 0, megjegyezzük, hogy a működése csökken, mint az egyik mozog a másik ága a hiperbola 0 + ∞, akkor azt látjuk, hogy a függvény növekszik.

Ha az egyenlet a másodfokú függvény vezető koeffitsienta = 1, akkor a grafikon a másodfokú függvény pontosan ugyanolyan alakú, mint az y (x) = x 2 bármely értékek többi együttható.

Ez a forma, és alapjául az „alap-pontok”:

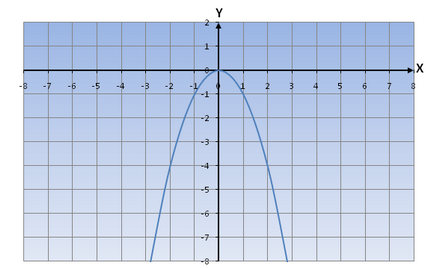
Parabola két részből áll: az egyik tárolja a negyedek III, ahol a negatív értékek az X és Y, és egy második rész - egy negyed I v ahol a pozitív értékek X és Y értékek negatívak.

y (x) <0, при x ∈ (-∞;0) ∪ (0;+∞)

Ha megy az egyik ága a parabola származó -∞ és 0, tudomásul vesszük, hogy a függvény növekszik, mint az egyik mozog a másik ága a hiperbola 0 + ∞, akkor azt látjuk, hogy a működése csökken.

1) a domain a funkció:

2) terület értékek:

3) A legnagyobb és a legkisebb érték a függvény:

Ha egy<0, то Yнаиб =0,Yнаим нет.

Ha a> 0, toYnaim = 0, Ynaib nem.

4) Y (X) = x 2 - páros függvény (t.k.f (-x) = x 2 = (- x) 2 = f (x)).

A grafikon szimmetrikus tengelyéhez képest oY.

5) A korlátozott funkciók:

Ha a> 0, alulról korlátos.

Ha egy<0 , функция ограничена сверху.

6) Funkció metszi oX oY tengelyen és a pontot (0, 0)

Mozgó parabolyy (x) = x 2

Ha ehhez hozzátesszük a konstans d (D ahol tetszőleges számú), mint egy summand hogy X mozgás fog bekövetkezni tengelye mentén a parabola (együtt a függőleges aszimptotával).

Ebben az esetben az egyenlet a függvény a következő lesz:

Ha D> 0 (y (x) = (x + d) 2). A függvény grafikonját mozog oX tengelyen a bal oldalon.

Vegyük például az y = (x + 2) 2

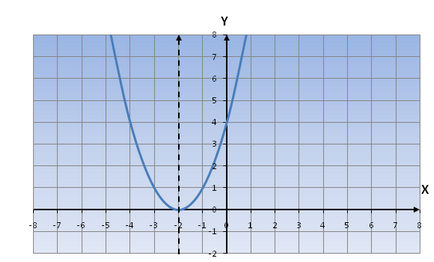
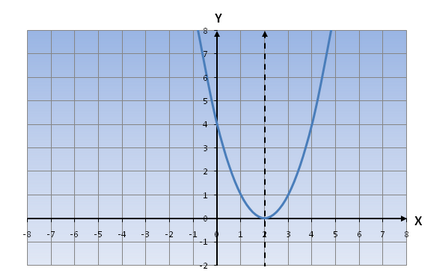
Ha d<0 (y(x)=(x-d) 2 ). то график функции передвигается по оси oX вправо.

Vegyük például az y = (X-2) 2

Ha ehhez hozzátesszük a c konstans (c ahol minden szám) a X2 mint összeadandó, nem lesz mozgás oY parabola tengelye (a vízszintes asymptote)

Ebben az esetben az egyenlet a függvény a következő lesz:

Ha c> 0 (y (x) = (x) 2 + c), majd a grafikont a funkció oY tengelyirányban mozog felfelé.

Vegyük például az y = (x) 2 +2

Ha c <0 ( y(x)=(x) 2 -c ), то график функции передвигается по оси oY вниз.

Vegyük például az y = (x) 2 -3

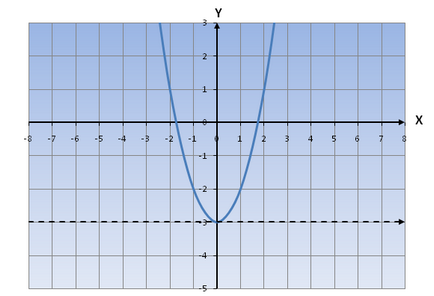
És megállapította, a gyökerek a diszkrimináló

1) 1) Ha D> 0, akkor a egyenlete ax 2 + bx + c = 0 két megoldás, az egyenlet y = ax 2 + bx + c 2 van egy metszéspontja tengelyével oX:

Ha a> 0, a grafikon funkció lesz a hozzávetőleges formában:

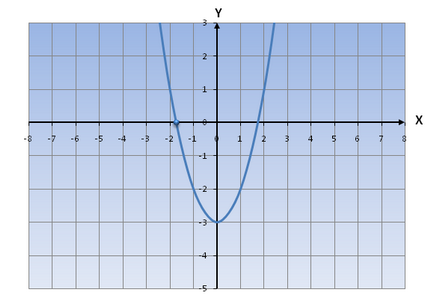
2) Ha D = 0, akkor az egyenlet ax 2 + bx + c = 0 van egy megoldás a 1 => uravneniey = ax 2 + bx + c 1 a metszéspont a tengellyel Ox.

Ha a> 0, a grafikon funkció lesz a hozzávetőleges formában:

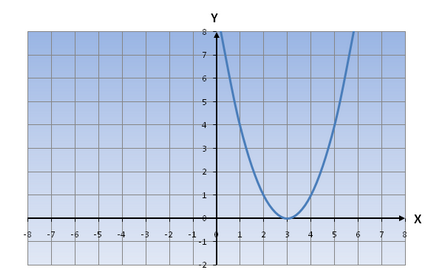
3) Ha D<0, то уравнение ax 2 +bx+c=0 не имеет решения, => uravneniey = ax 2 + bx + c nincs közös metszéspontot tengelyével Ox.

Ha a> 0, a grafikon funkció lesz a hozzávetőleges formában:

Koordinálja a csúcsa a parabola

Koordinátái a csúcsa a parabola keresztül a képletben:

A vonal áthalad a csúcsa a parabola a szimmetriatengelye a parabola.

A metszéspontja osyuoY

Mivel abszcisszán bármely pontján fekvő tengelyen oY nulla, hogy megtalálják a metszéspontja a parabola y = ax 2 + bx + c tengelyű oY, szükséges az egyenletben a parabola helyett Xpodstavit 0, akkor Y (0) = c.

Egy algoritmust szerkesztett másodfokú parabola

1) ágak irányba.

2) a koordinátáit a csúcsa a parabola.

3) A gyökerek a diszkrimináns.

4) Kiegészítő pont.

5) építése a grafikonon.

Construct függvényében y = x 2 -6x + 15

A kvadratikus trinomiális x 2 -6x + 15, hogy kifejezze a négyzetes különbség képlet segítségével Rövidítés szorzás.

Az alapvető képlet: (a ± b) = x 2 2 ± 2ab + b 2.

Mi kifejezetten a négyzetes különbség: x 2 -6x + 15 = (x 2 -6x + 9) +6

Elhelyezés a képlet: (x 2 -6x + 9) + 6 = (X-3) 2 +6

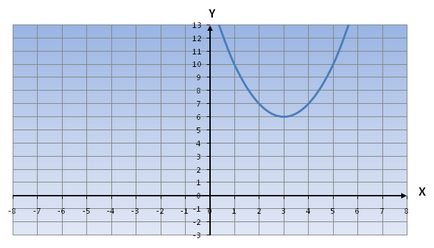
Kapunk egy függvény az y = (X-3) 2 +6

Megjegyezzük, hogy a függvény grafikonját eltoljuk 3 Ox tengely jobbra, és 6 oY tengelyirányban felfelé.

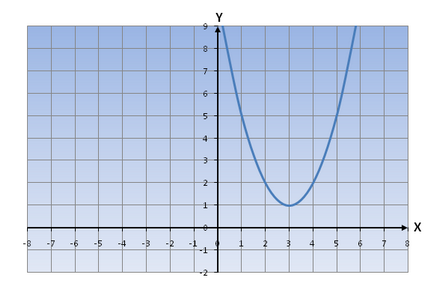
Következésképpen, a grafikon a függvény az y = (X-3) 2 6 nézne ki:

Construct függvényében y = x 2 + 8x + 17

A kvadratikus trinomiális x 2 + 8x + 17, hogy kifejezze a négyzetes különbség képlet segítségével Rövidítés szorzás.

Az alapvető képlet: (a ± b) = x 2 2 ± 2ab + b 2.

Mi kifejezetten a négyzetes különbség: x 2 + 8x + 17 = (x 2 + 8x + 16) +1

Elhelyezés a képlet: (x 2 + 8x + 16) + 1 = (x + 4) 1 2,

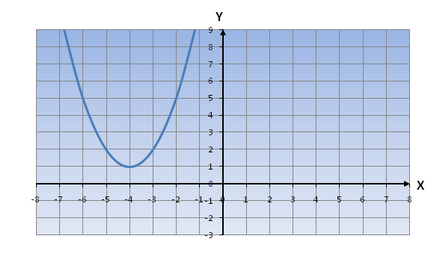
Kapunk egy függvény az y = (x + 4) 2 + 1,

Megjegyezzük, hogy a grafikon a balra tolódott 4 OX és 1 oY tengelyirányban felfelé.

Következésképpen, a grafikon a függvény az y = (x + 4) 1 2 nézne ki:

Bővíteni a tér trinomiális ezt az algoritmust:

1) kifejezetten a négyzetes különbség e trinomiális, képlet segítségével Rövidítés szorzás;

2) Elhelyezés, kapott képlet;

3) „olvasni” a grafikon egy eltolva koordinátájú tengelyeket;

4) össze egy grafikon.