Hogyan talál egy oldalsó derékszögű háromszög
Azt mondjuk, hogy ezek a komponensek (oldalfalak, szögek, stb) Határozza meg az ábra jól, ha egy másik alak a fenti komponenseket feltétlenül egyezik meg az eredetivel. Például, két oldalán a háromszög, és a köztük lévő szög, és a két oldalsó azzal szomszédos ferdén vagy három oldalról a egyenlősége alapján háromszögek egyedileg határozzuk meg minden háromszög. Vannak más esetek egyértelmű meghatározása háromszög egyenlő szárú háromszöget adatbázis és csökken a magasság háromszögek a három mediánjait háromszög adatok három magasságokban stb Nagyon fontos, hogy a probléma megoldásának, hogy meghatározzák a planimetrikus ábra világosan továbbra is úgy, hogy az ő ismeretlen alkatrészek, amelyek szükségesek a folytatása során a probléma megoldásának.
Ahhoz, hogy megtalálja az ismeretlen oldalai és szögei háromszög egyértelműen meghatározott általában használja a tétel a szinusz és koszinusz.
@
ahol R - sugara közelítőleg háromszög okruzhnosti.Teorema koszinuszok
Kiderül, hogy a meghatározó a szög a háromszög legjobb, hogy megtalálják a koszinusz mint sinus. Ez annak a ténynek köszönhető, hogy a szinusz nem tesz különbséget szögek: a koszinusz megkülönbözteti minden szögből 0 p. ahol hegyesszögben tartjuk ez pozitív a derékszög - egyenlő nullával, és a tompaszög - negatív, valamint a:.
Az alábbi példa az alkalmazás a szinusz és koszinusz-tétel megtalálása ismeretlen oldalai és szögei néhány egyedülálló háromszög. Legyen saját.
Válasz: a). , G = p - a - b;
b). , B = p - g - a;
@ Általános szabály, hogy ha megoldja a háromszög első igyekeznek meghatározni három oldalról, majd megtalálja a szükséges alkatrészeket. Az ismert három oldalán a háromszög, hogy pontosabban rajz az áttekintő képet kell tudni, hogy milyen típusú a háromszög (a hegyesszögű, derékszögű vagy tompaszögű).
A képlet eredő koszinusz-tétel alkalmazható a legnagyobb szöget, figyelembe véve a jele a koszinusz, megkaphatjuk a kapcsolat a oldalán a tér, amely lehetővé teszi, hogy meghatározzuk a formájában egy háromszög.
Következésképpen a háromszög ahol c - legnagyobb párt, tompaszög, ha; hegyesszögű, ha és téglalap alakú, amikor.
Gyakorlat 6 2.2.
Hosszában a három oldalán a háromszög határozza meg a típus:
Megjegyzés. Ismeretes, hogy ellen nagyobb oldala a háromszög nagyobb szögben, és fordítva. Koszinusz nagyobb szög megtalálható a képletből, a következő tétele koszinuszok.
Válasz: a) és b) téglalap alakú, b) tompa, d) hegyesszögű, stb) nem létezik.
A kapcsolat a testmozgás 6.2.2. d) meg kell jegyezni, gyakran alkalmazott megoldása geometriai problémák az úgynevezett háromszög-egyenlőtlenség. @ Három szegmens alkot háromszöget akkor és csak akkor, ha az összeg a hossza a kisebb hosszabb, mint a nagyobbak.
Még egy másik megvalósítási mód szerint a készítményt használjuk a háromszög egyenlőtlenség: Minden három pontot az A, B és C h AB - BC AC chЈ J AB + BC; ahol a jobb oldali egyenlőtlenség válik egyenlőséget csak akkor, ha a B pont fekszik a szegmens AC; és a bal oldali egyenlőtlenség válik egyenlőség csak akkor, ha az A, B és C kolineáris és B pont nem tartalmazza a szegmens AC.
Most bemutatunk példákat megoldani bizonyos feladatokat a Kuban Állami Egyetem felvételi vizsgák.
Ennek alapján AC ABC háromszög. Ez kialakítva átmérőjű kör, amely metszi oldalán AB és BC az M és N pontok, ill. Keresse meg a kör sugarát, ha AB = a, és az AM = a. És CN = b. döntés
Tól egyenlő szárú háromszög AOM megtalálják P A = (p - a) / 2 egyenlő szárú háromszög, és a CON lelet P C = (p - b) / 2. Miért P B = p - P A - P C = (a + b) / 2.
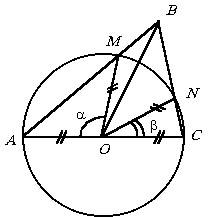
Jelentés megtalálása és B szögek abban a tényben rejlik, hogy az ABC háromszög, tudni fogjuk az AB oldal = egy és két szomszédos szögének, azaz D ABC egyértelműen meghatározott. Továbbra is találni ismeretlen AC oldal, mint a például a 6.2.1): és. Ha a kör sugara van.
Példa 6.2.4. (Kuban Állami Egyetem, Math. 1979)
Az ABC háromszögben beírt kör. Rámutat D, E, F - az érintési pont oldala AB, BC, CA, ill. Határozzuk meg az ABC háromszög területe. ha AB = a, BC = b, R DEF = 60 °.
Ez az utalás érdekes, hogy a D ABC szerinti érvelés az alábbiakban kerül meghatározásra egyedülálló. Ugyanakkor olyan összetevőkkel lehet, hogy nincs több, mint két különböző háromszög! döntés
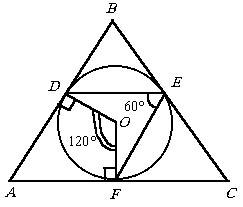
Legyen O - központ a beírt kör. Mivel DEF kerületi szög 60 °. Dof a központi szög 120 °. A szögek összege a négyszög ADOF egyenlő 360 °. Tehát tudjuk, hogy a ABC háromszög két oldala AB = a, BC = b. és az A szög (nem közöttük!).
Ezután arra törekszünk, hogy talál egy harmadik fél AC. Feltételezve, hogy AC = x, van koszinuszok és tétel. Location. Aztán találunk ABC háromszög területe formula.
A válasz nem egyértelmű!
Megjegyzés. Célszerű nem korlátozódik a válasz megoldásában az előző probléma.
Tehát, ha, (IE), a probléma nem megoldás.
Ha ugyanazt, vagy b> a. (Azaz, akár), akkor a probléma egy egyedi megoldást :.
Csak amikor (hogy) már korábban kimutatták, kétszámjegyű hozamot.
Most, a kérelmet a háromszög-egyenlőtlenség illusztrációk mutatom be a megoldást egy egyszerű feladat szóbeli vizsgák a matematika kar Kuban Állami Egyetemen.
Bizonyítsuk be, hogy az összeget a két mediánok egy háromszög kisebb, mint a kerülete. bizonyíték
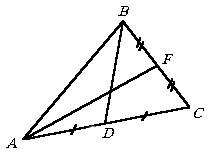
A háromszög-egyenlőtlenség D ABF és D ACF van AF
Ahol, analóg módon a D ABD és D CBD. 2 BD kapjunk <, а значит 2AF + 2 BD <2 и AF + BD <. что и требовалось доказать.
Igazoljuk, hogy bármely ABC háromszög D. bármely pontján fekvő belül, vagy az oldalára, a szegmens hossza kisebb, mint az AD semiperimeter ABC háromszög.
Megjegyzés: A érvek hasonlóak adott elején a bizonyíték a korábbi munkát.
Befejezésül a részben bemutatjuk a három tipikus feladatok megoldás, amely a fő szerepet játszott a tétel a koszinuszok.
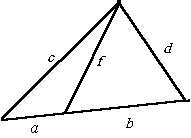
Annak illusztrálására, dönt a).
a) Adott: a, b, c, d. Keresse f.
b) Adott: a, b, c, f. Keresse d.
c) Adott: a, c, d, f. Keresse b.
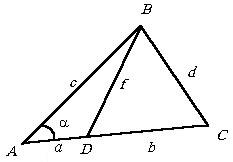
Bemutatjuk továbbá P A = a. D ABC lelet
.
Ezután a D ABD találni.
azaz .
Feladatok b) és c) dönt a saját. Figyeljük meg, hogy a megoldás a b), mint az a), csak az egyik érték a szegmensben ismeretlen hosszúságú, és a munkát) két lehetséges kívánt értékét b.
ELŐRE | Vissza | FŐOLDAL | síkrajzi | szeterometria