Hogyan lehet megoldani a problémát a másodfokú függvény

Válasz :. nullák «y = x 2 - 3" x1 = √ 3; x2 = - √ 3.

Hogyan talál, amit értékek «x» másodfokú függvény a megadott számérték

Ahhoz, hogy megtalálja, amit értékek «x» másodfokú függvény elfogad egy előre meghatározott számérték van szüksége:

• helyett «y» helyettesítő funkciója egy meghatározott számérték;
• oldja meg a kapott másodfokú egyenlet «x».

, Amelyeknek az értékei a «x» funkció «y = x 2 - x - 3" értéket veszi "-3".

Mi helyettesíti az eredeti funkciója «y = x 2 - x - 3" helyett«y = -3», és megtalálja«X».

y = x 2 - x - 3

-3 = x 2 - x - 3
x 2 - x - 3 = -3
x 2 - x - 3 + 3 = 0
x 2 - x = 0
x1; 2 =

1 ± √ január 02-04 · 1 · 0

Válasz: A «x = 0» és a «X = 1" funkció« y = x 2 - x - 3" értéket veszi «y = -3».

Hogyan lehet megtalálni a koordinátákat a parabola és a vonal metszéspontjai

Ahhoz, hogy megtalálja a metszéspontja a parabola a vonal van szükség:

• egyenlővé a jobb oldalán a funkciók (funkciók azon részei, amelyek a «x»);
• oldja meg a kapott egyenletet «x»;
• Behelyettesítve a számértékek «x» minden olyan funkciót, és segítenek megtalálni a pontok koordinátáinak a „Oy” tengelyen.

Keresse meg a koordinátáit metszéspontja a parabola «y = x 2" és közvetlen«y = 3 - 2x».

Egyenlővé jobb oldalán funkciók és megoldani a kapott egyenletet «x».

2 = X 3 - 2x
X 2 - 3 + 2x = 0
x 2 + 2x - 3 = 0
x1; 2 =

2 ± √ február 2-04 · 1 + (-3)

Most helyettesít semmilyen előre meghatározott funkciók (például, «y = 3 - 2x») kapott számértéket «X», hogy megtalálják a koordinátákat «y» metszéspontok.

1) X = 3
y = 3 - 2x
y (3) = 3 - 3 = 2 × 3-6 = -3
(·) A (3; 3) - az első metszéspontja.

2) x = -1
y = 3 - 2x
y (-1) = 3 - 2 · (-1) = 3 + 2 = 5
(·) B (1; 5), - a második metszéspontja.

Jegyezzük fel a metszéspont koordinátái válaszul.

Válasz: «y = x 2" metszéspontja a parabola és egy egyenes vonal«y = 3 - 2x»:
(·) A (3, -3) és (·) B (-1; 5).

Hogyan állapítható meg, hogy egy adott pont a parabola grafikon funkció tartozik

Tulajdonjogának igazolására a pont a parabola nem szükséges, hogy létrejöjjön egy függvény grafikonját.

Elegendő, hogy helyettesítse a pont koordinátáit a függvény képlet (koordinátája «Ox» tengely helyett «X», és a koordináta «Oy» tengely helyett «y») és az aritmetikai számításokat.

• Ha kapsz egy valódi egyenlőség azt jelenti, hogy az a pont tartozik a függvény grafikonját.
• Ha rosszra paritás, a lényeg, nem tartozik a menetrend függvényében.

Nem rendszer «y = x 2" a grafikon, hogy melyik pont tartozik hozzá: (+) A (2, 6). (·) B (1; 1).

Helyettesítő függvényében «y = x 2" pont koordinátáit (+) A (2, 6).

y = x 2
6 = 2 február
6 = 4 (helytelen)

Tehát, az a pont (+) A (2; 6) nem tartozik a grafikon a «y = x 2" .

Helyettesítő függvényében «y = x 2" koordináták pont (·) B (1; 1).

y = x 2
1 = (-) 1 február
1 = 1 (igaz)

Ennélfogva, a dot (·) B (1; 1) tartozik a grafikon a «y = x 2" .

Hogyan lehet megtalálni a metszéspontja a parabola a koordináta-tengelyek

Keresse meg a koordinátáit metszéspontja a parabola «y = x 2 -3x + 2" , hogy a koordináta-tengely.

Először egy függvényt definiálunk metszéspontja «Ox» tengelyen. A grafikonon a pontok a következők:

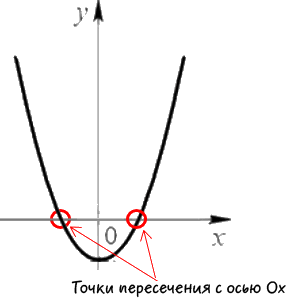
Amint az a fenti ábrán a koordináta «y» a «Ox» tengely metszéspontjait nulla, ezért helyettesíteni «y = 0" a kezdeti funkció« y = x 2 -3x + 2" , és megtalálja a koordinátáit «Ox» tengelyen.

0 = X 2 -3x + 2
-3x + x 2 2 = 0
x1; 2 =

± √ 3 március 2-4 · 1 · 2

Írunk a generált koordinátáit metszéspontok a «Ox» tengely: (·) A (2, 0) és (·) B (1, 0).

Most azt látjuk, a koordinátákat a metszéspont a tengely «Oy».

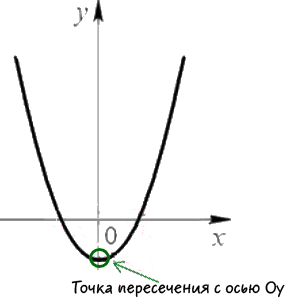
Amint az a fenti ábrán, a koordináta «x» keresztezi «Oy» tengely nulla.

Behelyettesítve «x = 0„az eredeti funkció «y = x 2 + 2 -3x„, és talál egy koordináta pontot «Oy» tengelyen.

y (0) = 0 2 - 3 × 0 + 2 = 2

Írja ki a egy pont koordinátáit kapjuk: (·) C (0, 2)

Írunk válaszul a koordinátáit metszéspontjai parabola tengely.

Válasz: «Ox» metszéspont a tengely: (·) A (2, 0) és (·) B (1, 0).
C «Oy» tengely: (·) C (0, 2).

Hogyan állapítható meg, hogy mi az x függvény pozitív vagy negatív értékeket

Felhívjuk figyelmét, hogy ha a feladat azt mondja: „úgy értékek” - ez egy „y” értékeket. Más szóval, meg kell válaszolni a kérdést: milyen értékek «x» összehangolják «y» pozitív vagy negatív.

Annak megállapításához, a funkciója a grafikon, ahol a függvény pozitív vagy negatív értékeket kell:

• megfeleljen közvetlenül pontok olyan helyeken, ahol a grafikon keresztezi a «Ox» tengely;
• meghatározzák egy pozitív vagy negatív értéket a függvény az intervallum a sorok között végzett;
• írja a választ minden időszakban viszonylagos «x».

A grafikon a másodfokú függvény ábrán válasz: Ha mi értékei «x» függvény 1) pozitív értékeket; 2) a negatív értékek.

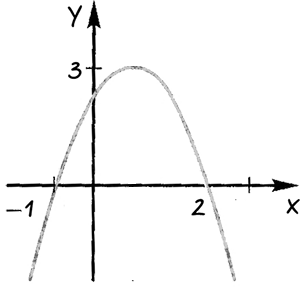
Keresztül a pontokat, ahol a függvény grafikonját keresztezi a «Ox» közvetlen tengely.

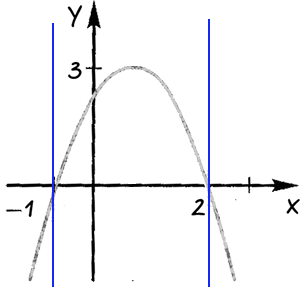
Mi határozza meg a régiót, ahol a függvény pozitív vagy negatív értékeket.

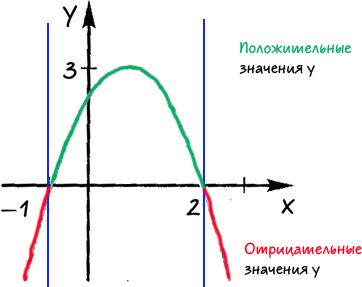
Bejelentkezés az egyes, a kapott terület, amelynek értéke «x» az egyes kiválasztott területeken.

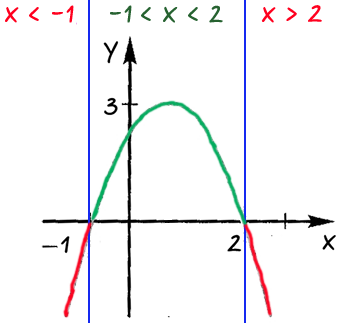
Válasz: A «x 2" függvény negatív értéket; ha „-1