Hogyan hozzunk létre egy mátrixot 1

Meghatározása a mátrix és annak elemei. Megnevezések.

Mátrix - egy táblázatot a $ m $ rows és $ n $ oszlopokat. A mátrix elemei lehetnek meglehetősen változatos természetét a tárgyak: számok, változók, vagy például, más mátrix. Például a mátrix $ \ left (\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right) $ tartalmaz 3 sorból és 2 oszlopból; elemei egész számok. A mátrix $ \ left (\ kezdeni a ^ 2 + 9 9 \ Sin x \\ -9 3t ^ 2-4 u-t 8 \ end \ right) $ tartalmaz 2 soros és 4 oszlopos.

Különböző módon Felvétel mátrixok: mutatják \ elrejtése

A mátrix lehet írni nem csak a kerek, hanem szögletes zárójelben vagy dupla sorokat. Ie rögzítési jelenti alatt ugyanazt a mátrixot:

$$ \ left (\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right) \; \; \ Left [\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right]; \; \; \ Left \ Vert \ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right \ Vert $$

A terméket a $ m \ alkalommal n $ nevezik a méret a mátrix. Például, ha a mátrix 5 sort és 3 oszlopot, az egyik beszél, a mátrix mérete $ 5 \ alkalommal 3 $. A mátrix $ \ left (\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right) $: $ 3 \ alkalommal 2 $.

Tipikusan a mátrix jelöli betűk a latin ábécé: $ A $, $ B $, $ C $ és így tovább. Például a $ B = \ left (\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right) $. Sorszámozás megy fentről lefelé; oszlopok - balról jobbra. Például, az első sor a mátrix $ B $ tartalmaz elemeket az 5. és a 3., valamint a második oszlop tartalmazza az elemeket 3, -87, 0.

mátrix elemek általában jelöljük kis betűkkel. Például, a mátrix elemei jelöljük $ A $ $ a_ $. Dual Index $ $ ij információkat tartalmaz a helyzet az elem a mátrixban. A szám $ i $ - ez a sor számát, és a számot $ j $ - oszlop számát, ami található a kereszteződésekben a eleme $ a_ $. Például, a kereszteződésekben a második sorban, és az ötödik oszlop a mátrix $ A = \ bal (\ kezdődik 51 37 -9 0 9 97 \\ 1 2 3 41 59 6 \\ -17 -15 -13 -11 -8 -5 \\ 52 31 -4 -1 17 90 \ end \ right) $ egy eleme $ a_ = $ 59:

Hasonlóképpen, a kereszteződésekben az első sor és az első oszlop eleme van $ a_ = $ 51; a kereszteződésekben a harmadik sorban, és a második oszlop - elem $ a _ = - $ 15, és így tovább. Megjegyezzük, hogy a rekord $ a_ $ olvasni, mint „két és három”, de nem „a harminckét”.

A rövidített jelölése mátrix $ A $, amelynek mérete megegyezik a $ m \ alkalommal n $, használt rögzítési $ A_ $. Ez lehet írott és telepített még néhány:

ahol rögzítési $ (a _) $ jelölés azt jelenti, mátrix elemeinek $ A $. A teljesen kitágult formájában mátrix $ A _ = (a _) $ felírható:

$$ A _ = \ left (\ begin a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \ end \ right) $$

Bemutatjuk egy másik kifejezést - Egyenlő mátrixban.

Két mátrixok azonos méretű $ A _ = (a _) $ és $ B _ = (b _) $ azt mondta, hogy egyenlő. ha az illető elem egyenlő legyen, azaz, $ A_ = B_ $ minden $ i = \ overline $ és $ j = \ overline $.

Felvétel "$ i = \ overline $" azt jelzi, hogy a paraméter $ i $ változó, 1 m. Például, a megtakarítás $ i = \ overline $ azt jelzi, hogy a paraméter $ i $ veszi értéke 1, 2, 3, 4, 5.

Így az egyenlőség, a mátrixok szükséges teljesítéséhez két feltétele van: akkora, mint egy meccs, és az egyenlőség a megfelelő elemeket. Például a mátrix $ A = \ left (\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right) $ nem egyenlő a mátrix $ B = \ left (\ kezdődik 8 -9 \\ 0 -87 \ end \ right) $, mivel a mátrix $ A $ jelentése $ 3 \ szor $ 2, és a mátrix mérete $ B $ 2 $ \ alkalommal $ 2. Szintén mátrix $ A $ mátrix nem egyenlő $ C = \ left (\ begin 5 3 \\ 98 -87 \\ 8 0 \ end \ right) $, mert a $ a_ \ neq c_ $ (azaz $ 0 \ neq $ 98). De a mátrix $ F = \ left (\ begin 5 3 \\ 0 -87 \\ 8 0 \ end \ right) $ nyugodtan levelet $ A = F $ a és méretű, és a megfelelő elemek a mátrixok $ A $ és $ F $ egybeesik.

Határozza meg a mátrix méretét $ A = \ left (\ -1 ​​kezdődik -2 1 \\ 5 9 -8 -6 \\ 8 23 \\ 11 -12 -5 \\ 4 0 -10 \\ \ end \ right) $. Jelzi, hogy milyen azok az elemek $ a_ $, $ a_ $, $ a_ $.

Ez a mátrix tartalmaz 5 sort és 3 oszlopot, így a mérete a $ 5 \ alkalommal 3 $. Mert ez a mátrix, akkor is használja a nevet $ $ A_.

$ A_ $ elem kereszteződésénél található az első sor és a második oszlop, azonban $ egy _ = - $ 2. Element $ a_ $ található metszi a harmadik sorban, a harmadik oszlop, így a $ a_ = $ 23. $ $ A_ elem kereszteződésénél található a negyedik sor, és a harmadik oszlop, így $ egy _ = - $ 5.

Típusú mátrixok méretüktől függően. Fő és másodlagos átlós. Trace egy mátrix.

Tegyük fel, hogy egy bizonyos mátrix $ A_ $. Ha a $ m = 1 $ (a mátrix áll egy vonal), az előre meghatározott mátrix egy mátrix sor. Ha a $ n = 1 $ (mátrix egy olyan, egyetlen oszlop), majd egy mátrixot nevezzük oszlopon mátrixot. Például a $ \ left (\ -1 ​​kezdődik -2 0 -9 8 \ end \ right) $ - sor mátrix és $ \ bal (\ kezdődik -1 \\ \\ 5 6 \ end \ right) $ - oszlop mátrix.

Ha a mátrix $ A_ $ true állapotban $ m \ neq n $ (azaz, a sorok száma nem egyenlő az oszlopok száma), ez gyakran azt mondta, hogy a $ A $ - derékszögű mátrix. Például a mátrix $ \ left (\ -1 ​​kezdődik -2 0 9 \\ 5 9 5 1 \ end \ right) $ 2 $ \ alkalommal $ 4, azaz a Ez magában foglalja a 2 soros és 4 oszlopos. Mivel a sorok száma nem egyenlő az oszlopok száma, ez a mátrix téglalap alakú.

Ha a mátrix $ A_ $ true állapotban $ m = n $ (azaz, a sorok számát megegyezik az oszlopok száma), akkor azt mondjuk, hogy a $ A $ - négyzetes mátrix érdekében $ N $. Például a $ \ left (\ -1 ​​kezdődik -2 \\ 5 9 \ end \ right) $ - négyzetes mátrix másodrendű; $ \ Left (\ -1 ​​kezdődik -2 9 \\ 5 9 8 \\ 1 0 4 \ end \ right) $ - négyzetes mátrix a harmadik rend. Általában a négyzetes mátrix $ A_ $ felírható:

$$ A _ = \ left (\ begin a_ a_ \ ldots a_ \\ a_ a_ \ ldots a_ \\ \ ldots \ ldots \ ldots \ Ldots \\ a_ a_ \ ldots a_ \ end \ right) $$

Azt mondják, hogy az elemek $ a_ $, $ a_ $, $ \ ldots $, $ a_ $ található a fő diagonális mátrix $ A_ $. Ezek az elemek az úgynevezett fő átlós elemek (vagy egyszerűen átlós elemek). Elements $ a_ $, $ a_ $, $ \ ldots $, $ a_ $ oldalán található (másodlagos) képátlójú; nevezik őket oldalsó átlós elemek. Például, a mátrix $ C = \ left (\ begin2-291 \\ 598 0 \\ 1 0 4 -4 -7 \\ -9 5 6 \ end \ right) $ van:

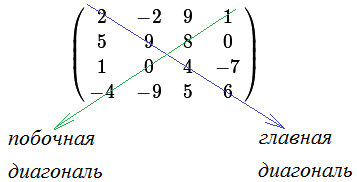
Elements $ C_ = 2 $, $ C_ = 9 $, $ C_ = 4 $, $ C_ = $ 6 fő átlós elemek; elemek $ C_ = 1 $, $ C_ = 8 $, $ C_ = 0 $, $ c _ = - $ 4 - oldalán átlós elemek.

Az összeget a fő átlós elemek az úgynevezett nyoma a mátrix és jelöljük $ \ Tr A $ (vagy $ \ Sp A $):

Például, a mátrix $ C = \ left (\ kezdődik 2 -2 9 1 \\ 5 9 8 0 \\ 1 0 4 -7 \\ - 4 -9 5 6 \ end \ right) $ van:

A koncepció a átlós elemek is használják nem négyzet alakú mátrixok. Például, a mátrix $ B = \ left (\ kezdődik 2 -2 9 1 7 \\ 5 -9 8 0 -6 \\ 1 0 4 -7 -6 \ end \ right) $ a fő átlós elemek $ B_ = 2 $, $ b _ = - 9 $, $ B_ = $ 4.

Típusú mátrixok értékétől függően az elemek.

Ha az összes mátrix elemeinek $ A_ $ egyenlő nullával, akkor ez a mátrix úgynevezett nulladik és általában betűvel jelöljük $ O $. Például a $ \ left (\ begin 0 0 \\ 0 0 \\ 0 0 \ end \ right) $, $ \ left (\ begin 0 0 0 \\ 0 0 0 \\ 0 0 0 \ end \ right) $ - nulla mátrixok.

Hagyja, hogy a mátrix $ A_ $ a következő:

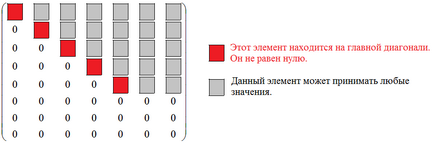
Akkor ez a mátrix az úgynevezett trapézizom. Nem tartalmazhat nulla sorok, de ha ezek, találhatók alján a mátrix. Általánosabban trapéz mátrix a következőképpen írható fel:

Ismét, a jelenléte nulla sorok végén nem szükséges. Ie műszakilag lehetséges kiosztani az ilyen feltételek trapéz mátrix:

1. Minden elem alatt található főátlójában nullával egyenlő.
2. Minden eleme a $ a_ $ a $ a_ $ feküdt a főátlójában nem egyenlő nullával: $ a_ \ neq 0 \; a_ \ neq 0, \ ldots, a_ \ neq 0 $.
3. Vagy az összes elem már $ m-R $ sorok egyenlő nulla vagy $ m = R $ (azaz nulla sorok nincs jelen egyáltalán).

Példák trapéz mátrixok:

Azt viszont, hogy a következő meghatározást. $ Matrix $ A_ nevű sebességet. ha megfelel a következő feltételeknek:

1. Az első elem az első sor nem nulla, $ a_ \ neq 0 $.
2. Minden nem nulla karakterlánc (azaz egy olyan karakterlánc, amely legalább egy elemet nem egyenlő nullával) áll két részből áll: az első (nulla), és egy második része, amely indul nemnulla elem:

A két nem nulla sorok alatt, amelyben nulla gyakran több.

Null vonal lehet elhelyezni csak a nem nulla sorok.

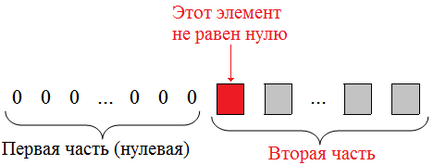
Például, lépés mátrix lesz:

Összehasonlításképpen, a mátrix $ \ left (\ begin 2 -2 0 1 \\ 0 0 8 7 \\ 0 0 4 -7 \\ 0 0 0 0 \ end \ right) $ nem egy lépést, mert a harmadik sorban a zéró ugyanaz, mint a második sorban. Ie Ez sérti az „alsó sorban - a nagyobb részét nulla.” Hozzáteszem, hogy a trapéz mátrix egy speciális esete egy lépcsős mátrix.

Azt viszont, hogy a következő meghatározást. Ha minden eleme egy négyzetes mátrix alatt elhelyezkedő fő diagonális nullával egyenlő, akkor ez a mátrixot nevezzük egy felső háromszög mátrixot. Például a $ \ left (\ begin 2 -2 9 1 \\ 0 9 8 0 \\ 0 0 4 -7 \\ 0 0 0 6 \ end \ right) $ - felső háromszög mátrix. Megjegyzendő, hogy az a felső háromszög mátrix semmit nem mond az értékek az elemek felett található a fő diagonális vagy a fő átlós. Lehetnek null vagy nem - ez nem lényeges. Például a $ \ left (\ begin 0 0 9 \\ 0 0 0 \\ 0 0 0 \ end \ right) $ - szintén egy felső háromszög mátrix.

Ha minden eleme egy négyzetes mátrix felett elhelyezett fő diagonális nullával egyenlő, akkor ez a mátrix az úgynevezett alsó háromszög mátrixot. Például a $ \ left (\ begin 3 0 0 0 \\ -5 1 0 0 \\ 8 2 1 \\ 0 5 4 0 6 \ end \ right) $ - alsó háromszög mátrix. Megjegyzendő, hogy az egy alsó háromszög mátrix nem mondtam semmit az értékek az elemek elhelyezve, vagy a fő átlós. Lehetnek null vagy sem - ez nem számít. Például a $ \ left (\ begin -5 0 0 \\ 0 0 0 \\ 0 0 9 \ end \ right) $ és $ \ left (\ begin 0 0 0 \\ 0 0 0 \\ 0 0 0 \ end \ right) $ - szintén alsó háromszög mátrix.

Egy négyzetes mátrix nevezzük átlós. ha minden eleme ennek a mátrix nem feküdt a fő átlós nulla. Példa: $ \ left (\ begin 3 0 0 0 \\ 0 -2 0 0 \\ 0 0 0 0 \\ 0 0 0 6 \ end \ right) $. A fő átlós elemek lehet bármilyen (nulla vagy nem) - ez nem lényeges.

A diagonális mátrix nevezzük egységet. ha minden eleme ennek a mátrix található a fő átlós egyenlő 1 Például a $ \ left (\ begin 1 0 0 0 \\ 0 1 0 0 \\ 0 0 1 0 \\ 0 0 0 1 \ end \ right) $ - az identitás mátrix negyedik sorrendben; $ \ Left (\ begin 1 0 \\ 0 1 \ end \ right) $ - az identitás mátrix a másodrendű.