Egyenlet három ismeretlennel, matematika

62. Egy egyenlet három ismeretlennel. Tegyük fel, hogy egy egyenlet

Ebben az egyenletben lehet tekinteni, mint egy rekord feladat: megtalálni számértékek x, y és z, hogy háromtagú 3x + 4y - 2z egyenlő volt a 11-es számú Tehát ez egy egyenlet három ismeretlennel. Tehát hogyan tudjuk megoldani az egyik egyenlet egy ismeretlen, hogy első látásra van a gondolat, hogy van két ismeretlen, mintha felesleges, és lehet adni tetszőleges értékeket. Valóban, ha például, hogy egy számot Y3 és Z az 5-ös szám, megkapjuk az egyenlet egy ismeretlen:

Vegyük más szám y és z. Tegyük fel például,

Akkor megkapjuk a következő egyenletet:

Folytatva ezt a munkát, akkor arra a következtetésre jutott:

Egy egyenlet három ismeretlennel, végtelen sok megoldás, és ez számukra kell adni két ismeretlen tetszőleges értékeket.

Ennek a munkát lehet írva a táblázatban (mi, kivéve a két már talált megoldást, rögzített ez egy másik, amelyet úgy kapunk, üzembe y = -1, és z = -2):

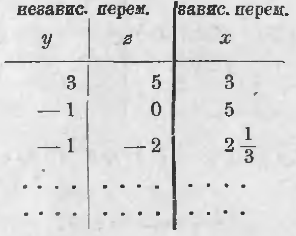
Mivel az y és z veszünk tetszőleges értékek, ezek a független változók, és x értéke függ (a) egy variábilis. Más szavakkal: x függvénye y és z.

Annak érdekében, hogy könnyebb megszerezni a megoldás ennek egyenlet, meg lehet határozni a x y, és z. kapjuk:

3x + 4Y - 2z = 11; 3x = 11 - 4Y + 2z;
X = (11 - 4Y + 2z) / 3.

Adunk, például. értékek: y = 5 és z = 1; kapjuk: x = (11-20 + 2) / 3 = -2 (1/3), stb ...

Vegyük az egyenlet

Tegyük fel, X és Y a független változók, és z - függőségek és meghatározni z keresztül x és y

-2z = 7 - 3x + 5Y; 2Z = 3x - 5Y - 7; Z = (3x - 5Y - 7) / 2

Most könnyű dönteni táblázat: