Bizonyítsuk be, hogy az átfogó hosszabb láb

Az átfogó egy derékszögű háromszög mindig nagyobb, mint bármely másik két oldala. Miért? Tény, hogy jön erre a következtetésre lehet több módon is.

Először is, ha tudjuk, hogy a másik viszont egy nagyobb szög mindig egy nagy párt, és két derékszögű háromszög közvetett éles szögben, a bizonyítás akkor meg nagyon egyszerű. Derékszög 90 ° és mellette fekszik átfogója. Akut szög kisebb, mint 90 °, így az oldalsó fekvő velük szemben (a lábak) kevesebb, mint egy derékszögű szemben fekvő átfogója.

A bizonyíték lehet építeni egy másik utat. Adott egy téglalap alakú ABC háromszög a derékszög A. Ebben az esetben, a másik két oldala pedig az AB és AC, és a hossza a átfogója BC.

Rajzold le a vonalszakasz BC BD egyenlő a lábát AB.

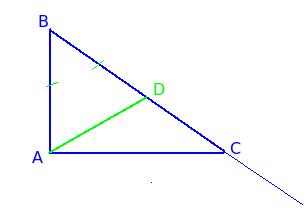
Ha a BC felett AB, a D pont nincs a átfogója BC, majd lábát a átfogója. Ha az AB kevesebb, mint a BC, majd a D pont fog feküdni az intervallumban a BC, ami kevesebb az átfogója lábát.

Tekintsük ABD háromszög. Ez egyenlő szárú mivel AB = BD által építése. Mint ismeretes a egyenlő szárú háromszögek a bázis szögek mindig hegyesszög. Tehát ∠BAD <∠BAC, так как ∠BAC прямой. Следовательно, луч AD лежит внутри угла ∠BAC и пересекает гипотенузу BC, то есть лежит на ней, а не за ее пределами. Поскольку доказано, что BD

Hasonlóképpen, ha bizonyítható, hogy a láb és az átfogó hálózati kevesebb, mint a BC, ha össze egy CD szakasz egyenlő AC.

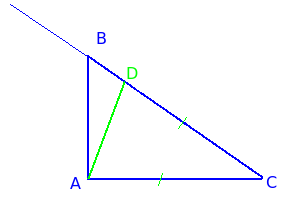
Itt ΔADC egyenlő szárú ∠DAC <∠BAC. Следовательно луч AD лежит внутри ∠BAC и пересекает отрезок BC.