Sinus és cosinus hogyan lehet megoldani

Megoldani egyszerű trigonometrikus egyenlőtlenségeket. . . (Ahelyett, hogy a címke lehet ..) használnak, grafikus módon. Keresse meg a metszéspont a grafikon a megfelelő funkciót vonalon. közelebb helyezkedik el a származási, majd a használt periodicitás a funkciót.

Bonyolultabb trigonometrikus egyenlőtlenségeket csökkenteni a legegyszerűbb esetben az egyszerűsítést.

Táblázatok és alapvető tulajdonságait a trigonometrikus függvények.

Táblázatok és alapvető tulajdonságait az inverz trigonometrikus függvények.

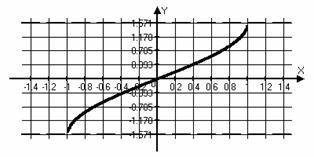
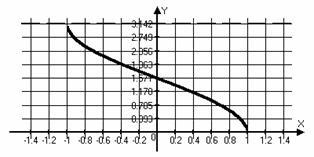
Funkció vagy akár, vagy páratlan

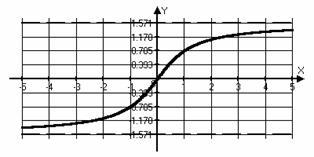
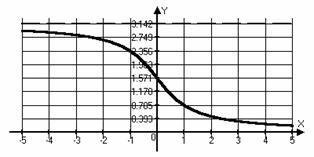
Funkció vagy akár, vagy páratlan

Kommunikációs trigonometrikus függvények inverz trigonometrikus függvények végzik az alábbi táblázat

Így a kifejezés értéke 0.

Magyarázat §: Solution trigonometrikus egyenletek és egyenlőtlenségek.

Hogy oldja önkényes trigonometrikus egyenletek és egyenlőtlenségek alkalmazni ugyanazon alapvető technikák korábban már leírták, hogy az oldat algebrai egyenletek: bevezetése egy új változó, és faktoring bal oldalán egy egyenlet vagy egyenlőtlenség.

Az általános megfontolások, az alábbiakat: felváltja egy funkció, hogy elkerülje bevezetése gyökök, mivel ez megnehezíti az oldathoz, és ellenőrzést igényel a gyökerek talált (az építőiparban a hálózati egyenlet tűnhet külső gyökerek).

Néha lehet, át az összes feltételt, hogy a bal oldalon az egyenlet, kiterítette a tényezőket.

1. egyenletek és viszonylag homogén.

Mindegyik egyenletek:

és ez homogén tekintetében. Az összeg a kitevők y és minden tagja ugyanazt az egyenletet. Ez az összeg az úgynevezett mértéke a homogén egyenlet. Elosztjuk. a mértéke a homogén egyenlet, lehet csökkenteni, hogy egy egyenletet tekintetében az algebrai.

Elosztják, például egyenlet. megkapjuk a következő egyenletet:

Ha ezeket az egyenleteket egyenértékű, mintha. akkor az első egyenletet kapjuk, hogy. hogy lehetetlen (és ugyanez az érv nem tűnnek). Ezután a egyenértékű egyenlet találunk. A másodfokú egyenlet megoldása. valamint azokra az értékekre - a megfelelő értékeket.

4. egyenlet megoldásához:

Határozat. És cseréje. Kapjuk homogén egyenletet:

Bemutatjuk az új változó, és kapunk egy másodfokú egyenlet érte:

A gyökerek az egyenlet. Ezután megkapjuk az egyenértékű egyenletrendszer:

2. egyenletek, balra, amely bomlik tényezőket, és a jobb oldalon nulla.

Átvitele az összes feltételt bármely egyenletnek a bal oldalon, ez lehet csökkenteni formájában.

Ha a bal oldali Ennek az egyenletnek bomlik tényezők, amelyek mindegyike nulla, és az egyenlet bomlik le néhány egyszerű egyenletek. Fontos szem előtt tartani, hogy a gyökerek az eredeti egyenlet csak azok a gyökerei egyenletek kapott tartozó domain az eredeti egyenlet.

5. Oldja meg az egyenletet:

Határozat. Itt célszerű használni az átalakulás képletek trigonometrikus függvények működik összeget. Ezekkel a képletekkel, megkapjuk a következő egyenletet:

A különbség koszinusz transzformáció egy termék. amely egyenértékű a készlet egyenletek:

Ezek az egyenletek megoldhatók révén univerzális trigonometrikus cserélni. képlet segítségével és kifejező keresztül.

Az eredeti egyenletet csökken a racionális algebrai egyenlet, amelynek megoldása már korábban tárgyaltuk.

Az ilyen egyenletek megoldódott bevezetésével racionálisabb Kiegészítő szöget :. Tekintsük a további megoldása során az egyenlet révén egyenértékű átalakulások bal oldalán:

Megjegyezzük, hogy a kifejezés zárójelben ebben az esetben átalakíthatjuk koszinusza a különbség az érvek:

Így az eredeti egyenlet ekvivalens az egyszerű trigonometrikus egyenlet:

amelynek megoldása, amelyek

A probléma megoldódott általános formában.

6. egyenlet megoldásához:

Bemutatjuk az új változót: és, egyenértékű másodfokú egyenlet.

amelyben a diszkrimináns nulla, és ezért egyetlen gyökere. A probléma megoldása csökken a következő egyenletet:

Határozat. (Második módszer). Bemutatjuk a kiegészítő szög :.

Ezután az oldatot az eredeti egyenlet egyszer írott formában:

Más szóval, megvan ugyanaz a válasz, ami nem meglepő.