Összegzés Az egyes szekvenciák

ezért
1 2 + 2 2 + 3 2 +. + N 2 = (n 3 + n 2 + (1 + 2 + 3 +. + N)) / 3.

mert
1 + 2 + 3 +. + N = n (n + 1) / 2,
1 2 +2 2 + 3 2 +. + N 2 = (n 3 + n 2 + n (n + 1) / 2) / 3 = n (n + 1) (2 n + 1) / 6.

Az összeg a negyedik hatványa az első n szám kapott arab matematikus Al- Karadzhi (X-XI cc.). Ő építette oldalú négyzet (1 + 2 + 3 + + (n -. 1) + N). és ez - a másik tér (szomszédos sarokban, az első tér) egy oldalon (1 + 2 + 3 + + (n -. 1)). A különbség a két négyzetek gnomon amelynek szélessége n. egy nagy oldala egyenlő (1 + 2 + 3 + + (n -. 1) + n) = n (n + 1) / 2 A területet a Gnómon 2 n 2 (n + 1) / 2 - n 3 2 = n . Ha most egy négyzet egy oldala (1 + 2 + 3 + + (n -. 1)) hozzárendelni az azonos szélességű Gnómon (n - 1). annak terület (n - 1) 3. Továbbra ilyen módon, végül kap, hogy a tér az eredeti 1. A terület egy négyzet egy oldala (1 + 2 + 3 + + (n -. 1) + N). így oszlik gnomons, területeket, amelyek egyenlő n 3. (n - 1) 3. 3 3. 2 3. és a négyzet alakú területének a 1 = 1, 3. Így, 1 3 + 2 3 + 3 3 +. + N 3 = (1 + 2 + 3 +. + N) 2 = (n (n + 1) / 2) 2.

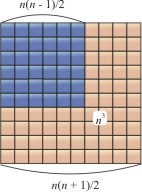
Ábra. 8. A seb területe gnomon n 3

Egy érdekes szekvencia tekinthető a francia skolasztikus filozófus XIV században. - N. Orem. Ő vajon mi egyenlő lenne az átlagos sebesség (a terminológia az átlagos „intenzitás”, egy általános kifejezés, de most elegendő ahhoz, hogy az átlagos sebesség) az intervallum 2, ha ezt az időtartamot szakaszokra oszlik megfelelő csökkenő mértani: 1, 1/2, (1/2) 2 (1/2) 3. és egyes szakaszaiban az arány növekszik egy számtani sorozat 1, 2, 3, 4. annak érdekében, hogy ezt a kérdést, meg kell, hogy értékelje a kifejezés az típus: 1 # X2219; 1 + 2 # X2219; (1/2) + 3 # X2219; (1/2) 2 + 4 # X2219; (1/2) 2. Az számának összege a Orem képviselt, mint a terület lépés-szerű alak, készült egymással szemben a téglalapok, amelyek mindegyike a magassága 1, és a szélessége az alsó 2, felette egy további 1/2. (1/2) 2 és a t. D. Az egész szám osztva függőleges vonalak darabokra szélessége 1, 1/2, (1/2) 2 és a t. D.

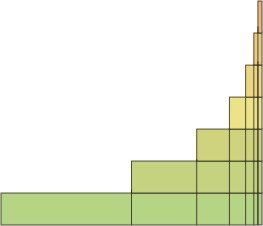
Ábra. 9. Több Orem

Ez a szám, sőt, nem más, mint a sebesség grafikon magassága a leghátsó bal oldali értéke 1, majd a 2, majd 3, stb az összeg több egyenlő a területet az egész szám, azzal a ténnyel együtt, hogy a terület megtalálható más módon ..: a téglalap területe egyenlő 2, a magasabb 1, majd 1/2 (1/2) 2, stb - .. mi nem foglalkozunk semmi más, mint egy mértani, amelynek összege egyenlő 4. az átlagos sebesség az egész intervallum egyenlő a teljes terület (4) osztva a hossza a rés (2) - azaz a 2, a sebesség a második rés. Korlátlanul csökkenő mértani és a szám tekinthető a Orem, véges mennyiségű. És a másik sorozat? Nyilvánvaló, hogy annak érdekében, hogy az összeg a végtelen számú szempontjából a sorozat egyenlő lenne egy véges érték, meg kell csinálni egy sor tagok általában nulla, azaz kezdve elég nagy számban, hogy kevésbé, mint az előre meghatározott értéket. De ez nem elég. Vannak, magukra, egy sorozat nullához, hogy az összeg a sorozat tart végtelenbe. Orem első bizonyítani, hogy a harmonikus sor

Nem summable, ez az összeg tagjainak n n növekedése előbb-utóbb meg fogja haladni bármilyen előre kijelölt értéket. A bizonyítás azon a tényen alapul, hogy a

1/3 + 1/4> 2/4 = 1/2,
1/5 + 1/6 + 1/7 + 1/8> 1/2,

8, és a következő számok összege több, mint 8/16 = 1/2, és így tovább. D. Egy, mivel számos 1 + 1/2 + 1/2 + 1/2 + és t. D. Nyilvánvalóan növeli a végtelenbe, és a harmonikus sor is tart a végtelenbe. Ezt a tényt néha alábbiakban mutatjuk be.

A téglákat helyeznek egymásra úgy, hogy azok nem tartoznak: erre tömegközéppontja a felső tégla belül kell lennie az alsó alap. Ha két tégla, az egyik tolható képest a másik felét a hossza. Ha három, majd a középső képest az alján el kell tolni egy negyedével, mert a tömegközéppontja a felső két félúton található a tömegközéppontjai egyes. Ha négy, majd tekintetében az alján a következő tégla kell eltolni egyhatoda a hossza egy tégla. És így tovább. D. Általában úgy tűnik, hogy korlátlan számú ideális tégla, a felső tolhatjuk aljához viszonyítva bármilyen távolságra a harmonikus sor kerülhet tetszőlegesen nagy értékre.

Amellett, hogy a végtelen mennyiségű lehet tekinteni végtelen termékeket. Az első közülük bevezetett F. Wyeth. Figyelembe véve a probléma A kör négyszögesítése, Wyeth hozta a kapcsolat a terület egy szabályos sokszög n és 2 n oldalú írva az azonos sugarú kör R. Mindegyik poligonok osztható 2 n háromszögek a vertex középpontjában a sokszög és a csúcsszöge, egyenlő 180 ° / n. az első közülük, minden egyes ilyen háromszög derékszögű, és a második egyenlőszárú. Mivel van egy közös magasságban, az arány a saját területek egyenlő az arány a bázisok. Az első bázis R cos (180 ° / n). a második terület arány R. sokszögek egyenlő a területek aránya ilyen háromszög t. e. cos (180 ° / n).

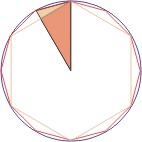
Ábra. 10. A terület aránya az aránya háromszögek bázisok