Optimális tervezés 1

A probléma, hogy amit most viszont a vita, az úgynevezett optimális tervezése. Létesítmények tervezése nagyon eltérő lehet a rendszer: a tevékenységek az egyes vállalat, ipar vagy a mezőgazdaság, a régió, végül az állam. Nyilatkozat a probléma a tervezés a következő:

• Vannak olyan célok: x, y, és mások;

• Vannak olyan források: R1, R2 és mások, ami miatt ezeket a célokat el lehet érni. Ezek a források szinte mindig korlátozott;

• van egy bizonyos stratégiai cél, ami függ az értékek az x, y, és egyéb célok, amelyeket el kell orientált tervezés.

Meg kell határozni az értékét célok figyelembevételével a korlátozott erőforrások függvényében elérésének stratégiai célokat. Ez lesz a legjobb terv.

Íme néhány példa. Hagyja, hogy a tárgy a tervezés óvoda. Mi szorítkozunk két tervszámok: a gyermekek száma és a pedagógusok száma. A fő forrásai az óvoda tevékenysége a méret a finanszírozás, és alapterület. Melyek a stratégiai célok?

Természetesen, az egyik ezek közül a megőrzése és erősítése a gyermekek egészségére. A kvantitatív ez a cél az, hogy minimalizáljuk az előfordulási óvodás.

Egy másik példa: a tervezés, a gazdasági tevékenységek az állam. Természetesen ez túl nehéz feladat számunkra, hogy teljes mértékben megérteni. Célok nagyon: ez a termelés volumene a különféle ipari és mezőgazdasági termelés, a terv a képzés, az összeget a villamos energia, a méret a fizetések a közszférában dolgozók, és így tovább. A források közé tartoznak :. száma munkaképes korú lakosság, az állami költségvetés, a természeti erőforrások, az energia, a lehetőséget a közlekedési rendszerek, stb Képzelheted, minden ilyen típusú források korlátozott. Ezen kívül a legfontosabb erőforrás az idő kiosztott végrehajtására vonatkozó tervet. A kérdés, hogy a stratégiai célok meglehetősen bonyolult. Az állam egy csomó őket, de különböző időszakokban a történelem, a prioritások céljainak változhat.

Ha azt akarjuk használni a számítógépet, hogy megoldja a problémát, az optimális tervezés, megint kell építeni egy matematikai modell segítségével. Ezért mindent, amit mondtam az elején ebben a szakaszban, le kell fordítani a számok nyelvén, képletek, egyenletek, és egyéb eszközök a matematika. Teljes egészében, ez a feladat nagyon nehéz valós rendszerekben. Mint korábban, hogy az utat az egyszerűsítés.

Vegyünk egy nagyon egyszerű példát, ahonnan kap egy ötletet az egyik megközelítés a probléma megoldásának az optimális tervezés.

Példa. Iskola cukrászda készíti torták és sütemények. Mivel a korlátozott tárolási kapacitás naponta, akkor főzni az aggregált legfeljebb 700 termék. Munkanap cukrászda 8 órán át. Ha a probléma csak sütemények, a nap lehet legfeljebb 250 darab pitét teheti 1000, ha nem termel sütemények. Az ára a torta kétszer magasabb, mint a pogácsa. Ez szükséges ahhoz, hogy a napi termelési terv, amely egy cukrászda a legtöbb bevételt.

Természetesen ez csupán egy esettanulmány. Nem valószínű, hogy van egy cukrászda is, amely csak két fajta termék, és aligha a legnagyobb bevételre - a célból, hogy a munkáját. Dolgozunk ki egy matematikai modellt a probléma.

vannak Cél:

x - napi torták ütemtervet;

a - napi sütemények ütemtervet.

Ebben a példában is lehet nevezni a termelési erőforrások? Abból a tényből, amint az a probléma állítás:

időtartamát a munkanap - 8 óra;

raktározási kapacitást - 700 ágy.

Feltételezzük, hogy az egyszerűség kedvéért a többi erőforrás (nyersanyag, villany, stb.) Nincs korlátozva. A formai gól - maximalizálja a bevételi részleg - megbeszéljük később.

Szerezze kapcsolatok, az alábbi feltételek időkorlátok, a műhely és raktár kapacitással, azaz a teljes cikkek számát.

A feltételek a probléma, ebből következik, hogy a gyártás cukrászati ​​töltött 4-szer hosszabb, mint a hogy a pite. Ha jelöljük a gyártási pite - t min, a gyártási idő lesz egyenlő 4t cake perc. Tehát a teljes időt a gyártó torták és sütemények is:

TH + 4ty = (x + 4Y) t.

De ezúttal nem lehet hosszabb, mint a munkanap. Ebből következik az egyenlőtlenségek

Könnyen kiszámítható t - a gyártás idején a tortából. Ami az időt a 1000 darab lehet, majd az egyik pogácsa töltött 480/1000 = 0,48 min. Behelyettesítve ezt az értéket az egyenlőtlenség, megkapjuk;

(X + 4Y) · 0,48 <= 480.

Korlátozását az összes termék ad teljesen egyértelmű egyenlőtlenséget:

A két kapott egyenlőtlenségeket kell hozzá szempontjából pozitív értékek az x és y (nem lehet negatív számú torták és sütemények). Ennek eredményeképpen kapunk egy egyenlőtlenségrendszer:

És most a formális stratégiai célok: maximalizálja a bevételek. Bevétel - az az érték, az összes eladott termékek. Tegyük fel, hogy az ár egy pite - r rubelt. A feladat szerint, az ár a torta kétszer, azaz 2r rubelt.

Figyelembe vesszük az írásbeli kifejezés függvényében x, y:

Ezt nevezik a célfüggvényt.

Mivel az R értékét - állandó, maximális értéke az f (x, y) elérésekor a maximális értéke (x + 2y). Ezért, mivel a célfüggvény lehet venni:

f (x, y) = x + 2y.
Következésképpen hogy szerezzen egy optimális tervet főtt le a következő matematikai probléma: találni értékű célokat x és y kielégítik az alábbi egyenlőtlenségeket a rendszer. amelynek értelmében a célfüggvény „vesz egy maximális értéket.

Így a matematikai modellje optimális tervezése az iskolai cukrászda épült.
Matematikai fegyelem, amely elkötelezett a problémának a megoldására, az úgynevezett matematikai programozás. Mivel az objektív függvény f (x, y) az x és y lineárisan (azaz, az első fokú), a probléma a részt ebben a tudomány néven lineáris programozás.

Egyenlőtlenségrendszer írva fent jelenik meg a koordinátarendszerben négyszög. által határolt négy megfelelő egyenes vonalak lineáris egyenletek:

x + y = 700;
X = 0 (y-tengely);

Ábra. 2,19, ez a terület egy ABCD és kiemelte kitölteni. Bármely pont a négyszög a megoldást a rendszer az egyenlőtlenségek. Például, egy ilyen pont az a pont a koordinátái x = 200, y = 100. értékének felel meg az f célfüggvény (200.100) - 400. A pont x = 600, y = 50 megfelel

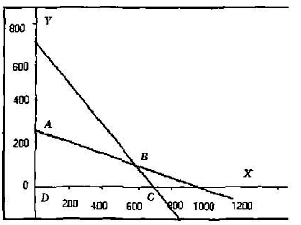
Ábra. 2.19. Terület keresni az optimális terv

F (600,50) = 700. De nyilvánvaló, hogy a kívánt megoldás az egyik terület ABCD pont, ahol a célfüggvény maximális. Megtaláljuk ezen a ponton végzünk lineáris programozási módszerek.

Ezek a gyakorlatok az MS Excel matematikai arzenál a következő részben meg fogja tanulni, hogyan kell használni őket.

A legfontosabb jellemzői

Optimális tervezés a célok meghatározása értékek Tekintettel a korlátozott erőforrások függvényében megvalósítása a stratégiai cél.

korlátozott erőforrások matematikailag képviseletében a rendszer egyenlőtlenségeket.

A formális stratégiai célkitűzések csökkenti az építőiparban a célfüggvény és célja bizonyos feltételeit annak mértéke, leggyakrabban elérése maximális vagy minimális.

Matematikai programozás - egy ága a matematika, amely módszereket problémák megoldására optimális tervezése.

Lineáris programozás - egy ága matematikai programozás, megoldása optimális tervezési probléma lineáris célfüggvény.

Kérdések és feladatok

1. a) Mi a probléma az optimális tervezés?

b) Melyek a célok, az erőforrások, a stratégiai cél? Adjon példát.

b) Mi a matematikai programozás, lineáris programozás?

3.a) Fogalmazza meg a probléma optimális megtervezésének ugyanazon a dll iskola cukrászda, amely termel három termék: piték, sütemények, kekszek.

b) Az első változás a készítmény optimális megtervezésének szálak 17 kétféle termék megfelel az akár egyetlen megszorítás feltételek: a több sütemény nem lehet kevesebb, mint a számos pitét. A koordinátarendszerben, építeni a keresési megoldás.

Semakin IG Henner EK Számítógépek és az ICT 11

Által küldött olvasó a weboldalak

Ha javításokat és javaslatokat a leckét, kérjük lépjen kapcsolatba velünk.

Ha azt szeretnénk, hogy a többi beállítást és javaslatokat órák, nézd meg itt - Oktatási fórum.