Megoldási módjait, egyenletrendszerek

Melyek a megoldási módjainak egyenletrendszerek?

Ebben a részben megbeszéljük három megoldási módjait, egyenletrendszerek. megbízhatóbb, mint a grafikus módszerrel, amely akkor volt az előző részben.

helyettesítő módszer

Ez a módszer akkor használható a 7. évfolyam megoldására rendszerek lineáris egyenletek. Az algoritmus, hogy alakult ki a 7. osztályban, elég megoldására alkalmas rendszerek egyenletek bármely két (nem feltétlenül lineáris) két x és y változót (természetesen változó lehet meghatározni, és a többi betű, ez nem számít). Tény, hogy ez az algoritmus már használják az előző pontban, ha a probléma a kétjegyű számot vezetett egy matematikai modellt, amely egy egyenletrendszer. Ez a rendszer a fenti egyenletekben, úgy döntöttünk, helyettesítő módszer (lásd. 1. példa 4. §).

Egy algoritmus segítségével a helyettesítési technika megoldására rendszer két egyenlet két változó x és y.

1. kifejezésre szempontjából x egy egyenletrendszer.
2. helyettesítve kifejezés y a többi egyenlet a rendszer.
3. Hogy oldja meg a kapott egyenletet x.
4. Helyettesítő felváltva mindegyik a gyökerek által talált az egyenlet a harmadik lépés helyett x az expressziós y x, kapott az első lépésben.
5. Record válasz formájában értékpárok (x, y), amelyek a vizsgálatok rendre a harmadik és a negyedik lépés.

Az x és y változót, természetesen, egyenlő jogokat, így ugyanolyan sikerrel tudjuk az első lépésben az algoritmus nem fejezhető x és x és y egy egyenlet. Általában válassza az egyenlet, amely egyszerűbb, és kifejezetten a változó belőle, amelyek az eljárás sokkal egyszerűbb.

1. példa megoldására az egyenletrendszert

1) kifejezni x y az első egyenlet: X = 5 - 3y.
2) Behelyettesítve ezt a kifejezést az x a második egyenletet: (5 - 3 a) y - 2.
3) Mi megoldjuk a kapott egyenletet.

4) Behelyettesítve váltakozva mindegyik a kapott értékeket az általános képletben Y jelentése X = 5 - Zu. Ha az
5) pár (2: 1), és az oldatokat adott egyenletrendszer.

algebrai addíciós módszerrel

Ez a módszer, mint a helyettesítő módszert, akkor jelentkezzen ki a tanfolyam Algebra 7. osztályban, ahol azt használják, hogy megoldja rendszerek lineáris egyenletek. A módszer felidézzük a következő példát.

2. példa Hogy oldja az egyenletrendszert

Szorozzuk minden tagja az első egyenlet 3, a második egyenlet változatlan marad:
Kivonjuk a második egyenlet az első egyenlet:

Ennek eredményeként, az algebrai hozzáadásával az eredeti rendszer a két egyenlet szerezni egy egyenlet egyszerűbb, mint az első és második előre meghatározott egyenletrendszer. Ez egy egyszerű egyenlet jogunkban cserélni bármely egyenlet az adott rendszer, mint a második. Akkor az adott egyenletrendszer helyébe egy egyszerűbb rendszert:

Ez a rendszer lehet megoldani helyettesítéssel. A második egyenlet helyettesíteni ezt a kifejezést az y az első egyenletben, megkapjuk

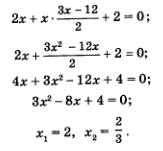
Továbbra is, hogy helyettesítsék a talált értékeket az x a képletben

Így azt találtuk, két megoldás van:

A módszer bevezetésének az új változók

A módszer bevezetése egy új változó megoldásában racionális egyenletek egy változót, akkor találkozunk során algebra 8. évfolyam. Ennek lényege, hogy a módszer megoldására egyenletrendszerek ugyanaz, de egy technikai szempontból, vannak olyan jellemzők, amelyek megbeszéljük a következő példák.

3. példa Hogy oldja az egyenletrendszert

Határozat. Bemutatjuk az új változó Aztán az első egyenlet átírható egy egyszerűbb formában: Oldjuk meg ezt az egyenletet a változó t:

Mindkét érték kielégíti a feltételt. és mivel a gyökerek racionális egyenletek változó t. De aztán, olyan, ahol azt látjuk, hogy az x = 2y, vagy
Így a módszer bevezetése egy új változó, mi lett volna képes, mintha „rétegződik” az első egyenletben a rendszer meglehetősen bonyolult megjelenésű, kettővel több, mint az egyszerű egyenlet:

Mi a következő lépés? És akkor mind a két egyszerű levezetett egyenletek viszont meg kell vizsgálni, hogy a rendszer az x 2 - y 2 = 3, ami még nem emlékeztetett. Más szóval, a probléma megoldása csökkenti a két egyenletrendszer.

Meg kell találni a megoldást az első rendszer, a második rendszer, és minden kapott egy pár értékek közé a választ. Nézzük megoldani az első sor egyenletek:

Az általunk használt módszer a helyettesítés, különösen azért, mert itt minden készen áll rá: 2y behelyettesıtve x a második egyenletben a rendszer. megkapjuk

Mivel x = 2y, azt találjuk, rendre x1 = 2, x2 = 2. Így előállított két oldatot adott rendszer (2, 1) és (-2, -1). Mi megoldjuk a második egyenlet:

Ismét használja a módszert a helyettesítés. 2 behelyettesıtve y a második egyenletben a rendszer. megkapjuk

Ez az egyenlet nincsenek gyökerei, ezért az egyenletrendszert nincs megoldása. Így a választ kell adni, hogy az csak az első rendszer megoldásokat.

A módszer bevezetésének új változók megoldására rendszer két egyenlet két használt változókat két kiviteli alak. Az első lehetőség egy új változót bevezetni és alkalmazni, csak egy egyenletrendszer. Ez volt a helyzet a példában 3.Vtoroy opció: két új változók bevezetésével és alkalmazásával egyidejűleg mindkét egyenletben a rendszer. Így lesz a helyzet a 4. példában.

4. példa Hogy oldja az egyenletrendszert

Két új változót:

Vegye figyelembe, hogy míg a

Ez lehetővé teszi, hogy átírják egy adott rendszer egy sokkal egyszerűbb formában, de tekintve, hogy az új változók a és b:

Alkalmazzuk az algebrai hozzáadásával eljárás megoldása a rendszer:

Mivel a = 1, akkor az egyenlet egy + 6 = 2 találunk: 1 + 2 = 6; 6 = 1. Így az a és b változó, van egy megoldás:

Visszatérve az x és y, megkapjuk az egyenletrendszert

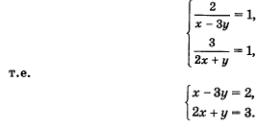
Alkalmazzuk az algebrai hozzáadásával eljárás megoldása a rendszer:

Mivel az egyenlet 2x + y = 3 találjuk:
Így az x és y, akkor van egy megoldás:

válaszolni:
Arra a következtetésre jutottunk ebben a részben egy rövid, de elég komoly, elméleti beszélgetést. Már kerestem némi tapasztalattal rendelkeznek a különböző egyenletek: lineáris, négyzetes, racionális, irracionális. Tudod, hogy az alapötlet az egyenlet megoldása a fokozatos átmenet az egyik egyenletet más, egyszerű, de egyenértékű a készlet. Az előző részben már bevezette a egyenértékűségének egyenletek két változó között. Használja ezt a koncepciót, és egyenletrendszerek.

Két rendszer egyenletek x és y változót nevezzük akkor ekvivalens, ha ugyanaz a megoldás, vagy ha a két rendszer nem megoldás.

Mindhárom módszer (helyettesítés, algebrai felül és az új változók), amelyet már ebben a szakaszban tárgyalt, ez teljesen korrekt a szempontból egyenértékűségét. Más szavakkal, ezeket a technikákat, akkor cserélje ki egy egyenletrendszer egy másik, egyszerűbb, de megegyezik az eredeti rendszer.

Grafikus módszer megoldására egyenletrendszerek

Van tanultál, hogy megoldja a rendszer egyenleteket, mint általános és megbízható módszerek, mint a helyettesítő módszer algebrai hozzáadásával és az új változók. És most emlékezzünk veletek egy olyan technika, amit már megtanult az előző leckét. Ez azt jelenti, hadd idézzem fel, amit tudni a grafikus módszer megoldást.

A megoldási módja az egyenlet rendszer grafikusan ábrázolja az egyes konkrét egyenletek szerepelnek ebben a rendszerben, és ugyanabban a koordinátarendszerben, valamint ahol erre szükség van, hogy megtalálják metszéspontjait E görbék. Ennek megoldására az egyenletrendszert a pont koordinátái (x; y).

Emlékeztetni kell arra, hogy az egyenletrendszert a grafikus hajlamosak akár egyetlen helyes megoldás, vagy végtelen sok megoldás vagy nincs megoldás.

Most mindegyik oldatból részletesebben. És így, az egyenletrendszert lehet az egyetlen megoldás, ha a közvetlen, amelyek grafikonok egyenletek metszik. Ha ezek a sorok párhuzamosak, akkor az egyenletrendszert egyáltalán nincs megoldás. Abban az esetben, véletlen a közvetlen horonyvágó egyenletrendszert, akkor egy ilyen rendszer lehetővé teszi, hogy megtalálja egy sor megoldást.

Most megnézi egy algoritmust megoldására rendszer két egyenlet 2 ismeretlenes grafikus módszerrel:

• Először is, az első építeni egy ütemtervet az 1. egyenlet;
• A második lépés a egy ütemtervet, amely tartozik a második egyenlet;
• Harmadszor, meg kell találnunk a metszéspontja a grafikonok.
• És a végén megkapjuk a koordinátáit minden metszéspont, melyik lesz az egyenletek megoldása.

Nézzük meg ezt a módszert részletesebben a példa. Adott egyenletrendszert kell megoldani:

1. Először is, mi fog építeni egy grafikont az egyenlet: x2 + y2 = 9.

De meg kell jegyezni, hogy az ütemezésnek megfelelően az egyenletek lesz egy kör, amelynek középpontja az eredetét, és annak sugara három.

2. A következő lépés a rajzoló ez az egyenlet, mint: y = x - 3.

Ebben az esetben meg kell építeni egy sort, és megtalálja azt a pontot (0, -3) és (3, 0).

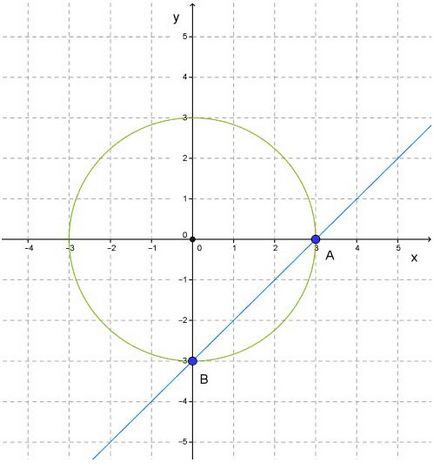
3. Lássuk, mit megvan. Látjuk, hogy a vonal metszi a kört két pont, A és B.

Most keresünk koordinátáit ezeket a pontokat. Látjuk, hogy a koordinátákat (3, 0) megfelelnek a A pont és a koordináták (0, -3), illetve B. pontjában

És mi lesz belőle, mint egy eredmény?

A kapott metszéspontja a vonal a kör (3, 0) és (0, -3) csak a két oldatot az egyenletek. Ebből következik, hogy az adatok számát is megoldás ezen egyenletrendszer.

Azaz, a válasz ez a döntés a következő: (3, 0) és (0, -3).