Matrix típusok mátrixok

Egység 1 elemei lineáris algebra

Mátrix típusú mátrixok. Műveletek mátrixok. mátrix elemeinek. Az inverz mátrixot

Meghatározás: A mátrix az úgynevezett négyszög elrendezésű számok álló m sorok azonos hosszúságú, vagy n oszlopok egyenlő hosszúságú.

aij - mátrix elem, amely az i-edik sorának és j-edik oszlop.

A főbb típusai a mátrix:

¾ négyzet alakú (a mátrix azonos számú sorok és oszlopok);

¾ átültetik (nyerhető megváltoztatásával a sorok és oszlopok a mátrix olyan helyeken A méretű mátrix ezen átalakítás lesz a dimenziója A mátrix T.);

¾ egység (négyzetes mátrixszal, az elemek a fő diagonális amelyek közül eggyel egyenlő, és a többi jelentése nulla)

Mátrixok széles körben használják a matematika egy kompakt rögzítési rendszer lineáris algebrai vagy differenciálegyenletek. Ebben az esetben a sorok számát a mátrixban megfelel számú egyenlet és az oszlopok száma - az ismeretlenek száma. Ennek eredményeként a megoldására rendszerek lineáris egyenletek csökken műveletek mátrixok.

következő algebrai műveletek vannak definiálva a mátrix:

¾ kívül mátrixok, amelynek ugyanolyan mérete;

¾ mátrix szorzás után a megfelelő méretű (egy olyan mátrix, oszlopok tud szaporodni a jobb oldalon egy olyan mátrix, sorok);

¾ beleértve szorzás mátrix vektor (a szokásos szabály mátrix szorzás vektor Ebben az értelemben, hogy a privát esetben a mátrix).

Tekintsük művelet mátrixok részletesebben.

1. mátrixok összeadása A + B a C mátrix a megállapítás működését, amelynek minden eleme páronként összege valamennyi releváns elemet a A és B mátrix, azaz minden egyes eleme a C mátrix egyenlő

2. Szorozzuk meg a számát a mátrix # 955; (Symbol: # 955; A) megépítésére a B mátrix, amelynek elemeit kapunk minden egyes elemét megszorozzuk a mátrix ezen az ábrán látható, azaz mindegyik elem a mátrix B egyenlő

3. Szorzás mátrixok (szimbólum: AB, kevesebb szorzás jele) - egy olyan művelet számítási C mátrix, amelynek elemeit az összegével egyenlő a termékek az elemek a megfelelő sorban az első szorzófokozat és a második oszlop (sor szorzás oszlop).

Az oszlopok száma a mátrix meg kell egyeznie a sorok számát a tömbben B. Ha az A mátrix méretükben. B mátrix -. akkor a dimenziója a termék AB = C. Lásd az 1. ábrát.

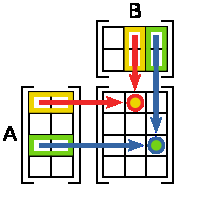
1. ábra - A szabály szorzás két mátrixok

1. példa: Find A + 2B, ha. .

2. példa: Find. if.

3. példa: A probléma megoldásához a mátrix-egyenlettel :,

.

Meghatározás: A determinánsát mátrix jelöljük: det (A), | A | vagy # 916; A.

A képlet a meghatározója a másodrendű:

Kiszámítására szolgáló képletek a determináns a harmadik rend:

a) bővítése a elemeinek az első sorban:

b) A csillaggal szabály (vagy Sarryusa)

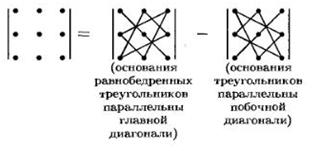
Az alapvető tulajdonságait determinánsok.

Az ingatlan 1. A determináns nem változott átültetése, azaz

Megjegyzés. A következő tulajdonságokat determinánsok lesznek formulázva csak húrok. Ha a tulajdonság azt jelenti, hogy 1 ugyanazokkal a tulajdonságokkal fog rendelkezni és oszlopok.

Az ingatlan 2. Ha megszorozzuk elemeit meghatározó vonal számos meghatározó szorozni ezt a számot, azaz a

Az ingatlan 3. A meghatározó amelynek null karakterlánc 0.

Az ingatlan 4 meghatározója, amely két egyenlő sorban 0.

Az ingatlan 5 meghatározó két vonal amelyek arányosak, nulla.

Az ingatlan 6. Amikor mozog a két sor a meghatározó, hogy megszorozzuk -1.

7. A tulajdonság értéke a meghatározó nem változik, ha az elemek az egyik sor, hogy adjunk megfelelő elemeivel egy másik sorban szorozva ugyanazt a számot.

8. meghatározása Minor megfelelő ez az elem aij a meghatározója a harmadik rend, úgynevezett másodrendű meghatározó kapott törlése Ezt a sort és oszlopot, amelyek metszete aktív elem, azaz a az i-edik sorának és j-edik oszlop. Kiskorúak aij megfelelő ez az elem fogja jelölni Mij.

4. példa: minor M12. A12 megfelelő elem. meghatározó lesz. amelyet kapott törlését meghatározója az 1. sor és a 2. oszlopban.

Definíció. Kofaktor az elem aij meghatározó hívják annak csekély Mij. szorozva (-1) i + j. Kofaktor aij elemet jelöli Aij.

A definíció azt látjuk, hogy a algebrai összefüggés fennállása között egy elem és komplementere által expresszált kisebb Aij = (-1) i + j Mij.

5. példa: Dan meghatározó. Keresse A13. A21. A32.

Definíció. Ha A - négyzetes mátrix, a fordított mátrix egy olyan mátrixkészítmény azt, jelöljük A -1 és megfelel annak a feltételnek. (Ez a meghatározás kerül bevezetésre, hasonlóan a szorzás számok). A koncepció egy inverz mátrix bevezetése csak négyzetes mátrixokra.

Tétel. Annak érdekében, hogy négyzetes mátrix Egy volt az ellenkezője, szükséges és elégséges, hogy a determináns lehet nullától eltérő.

Tehát, hogy megtalálja az inverz mátrix van szükség:

1. Keresse meg a meghatározója a mátrix

2. Keresse meg a mátrix transzponáltja a kapott mátrix.

3. Keresse cofactors Aij A mátrix elemeinek és T össze egy mátrix, amelynek elemei a számok Aij.

4. Szorozzuk meg a mátrix 3. lépésben kapott

6. példa: megtalálni a fordított mátrix A -1. ha majd érvényesítse.

. . Ahhoz, hogy ellenőrizze a használt képlet. hol.