másodfokú függvény

• egy másodfokú függvény olyan függvény a y = ax 2 + bx + c, ahol a, b, c - számok egy ≠ 0.
• A grafikon egy másodfokú függvény egy parabola.

A konstrukció a grafikont a funkció y = x 2 egy táblázatot az értékek

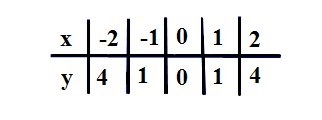
és a telek adatok felhasználásával pontot:

Figyelem! Ha az egyenlet a másodfokú függvény vezető együttható a = 1, akkor a grafikon a másodfokú függvény pontosan ugyanolyan alakú, mint a függvény grafikonját y = x 2 bármely értékek többi együttható.
A grafikon y = -x 2 a formája:

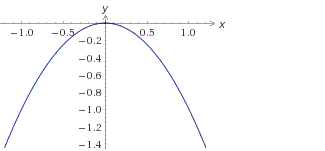
Tehát:
• Ha a magas együtthatója a> 0, akkor az a parabola szára napravleny fel.
• Ha a legmagasabb együttható egy 2 + bx + c meg kell oldani a másodfokú egyenlet ax 2 + bx + c = 0.

A folyamat során a másodfokú egyenlet megoldása, találjuk a diszkrimináns: D = b 2 -4ac, amely meghatározza a számát gyökerei egy másodfokú egyenlet.

Itt három lehetőség van:
1. Ha nincs D 2 + bx + c = 0 megoldások, és így a parabola y = ax 2 + bx + c nincs metszéspontot az x-tengely.
Ha a> 0, akkor a függvény grafikonját így néz ki:

2. Ha D = 0, akkor az egyenlet ax 2 + bx + c = 0 az egyik megoldás, és ezért a parabola y = ax 2 + bx + c egyetlen metszéspontja az x-tengely.
Ha a> 0, akkor a függvény grafikonját így néz ki:

3. Ha D> 0, akkor az egyenlet ax 2 + bx + c = 0 két megoldás, és ezért a parabola y = ax 2 + bx + c két metszéspontot az x-tengely :,
Ha a> 0, akkor a függvény grafikonját így néz ki:

Annak ismerete, az irányt a parabola ágait és a jel a diszkrimináló, akkor nagyjából meghatározni a megjelenés a grafikon a mi funkciót.

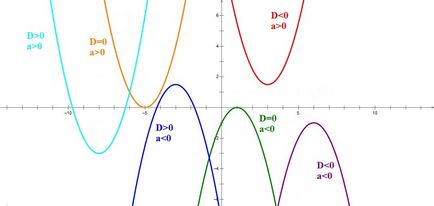
A következő fontos lépéseként a grafikont a másodfokú függvény - koordinálja a csúcsa a parabola:

A sort a csúcsa a parabola prohdyaschaya tengelyével párhuzamosan OY a szimmetriatengelye a parabola.

És egy lépésben a rajzoló funkciókat - a metszéspontja a parabola y = ax 2 + bx + c, hogy a OY tengelyre.

Mivel az abszcissza a tetszőleges pontot a OY tengelyen egyenlő nullával, hogy megtalálják a metszéspontja a parabola y = ax 2 + bx + c a OY tengellyel, szükség van az egyenletben a parabola helyett helyettesítjük nulla x: y (0) = c.

Azaz, a metszéspont a parabola tengelyével OY a koordinátái (0; c).

Így a fő pontok ábrázolásával kvadratikus függvények az alábbi táblázat mutatja: