Másodfokú függvény 3

Tér trinomiális polinom második fokozat, amely kifejeződése formájában ax 2 + bx + c. ahol a ≠ 0, b. c - (általában előre meghatározott) valós számok, nevezzük együtthatók, x - változó.

Megjegyzés: az arány lehet bármilyen valós szám nullától. Valóban, ha a = 0, akkor ax 2 + bx + c = 0 · x 2 + bx + c = 0 + bx + c = bx + c. Ebben az esetben a kifejezés még nem tér, így nem tekinthető egy négyzet trinomiális. Azonban, az ilyen-binomials kifejezéseket, mint például, 3x 2 - 2x vagy x 2 + 5 lehet tekinteni, mint egy négyzet trinomiális ha kiegészíti azokat a hiányzó egytagú nulla együtthatók: 3x 2 - 2x = 3x 2 - 2x + 0, és x 2 + 5 = x 2 + 0x + 5.

Ha a feladat meghatározni az értékét az x változó. amelyben négyzet trinomiális nullává válik, azaz a ax 2 + bx + c = 0, akkor van egy másodfokú egyenlet.

Ha vannak valós gyökerek X1 és X2 egy másodfokú egyenlet, a megfelelő trinomiális bontható lineáris faktorok. ax 2 + bx + c = a (x - x1) (x - x2)

Megjegyzés: Ha a négyzet trinomiális venni a forgatáson a komplex számok, amelyek talán még nem vizsgálták, a lineáris tényezőt lehet bővíteni minden alkalommal.

Ha egy másik feladat, hogy meghatározzuk az összes értéket, hogy el tudja fogadni az eredmény kiszámításánál a tér trinomiális különböző értékei esetén x. azaz y meghatározni az expressziós y = ax 2 + bx + c. akkor kell foglalkozni a másodfokú függvényt.

Ebben az esetben, a gyökerek egy másodfokú egyenlet a nullák egy kvadratikus függvény.

Szögletes trinomiális is felírható, mint

Ez a nézet akkor hasznos, ha rajzoló és tanulmányozása tulajdonságait kvadratikus függvények egy valós változó.

Függvény egy másodfokú függvény a következő képlet adja y = f (x), ahol f (x) - négyzet trinomiális. Ie képlet az űrlap

ahol a ≠ 0, b. c - bármely valós számokat. Vagy átalakítani egy általános képletű, például

.

A grafikon a másodfokú függvény egy parabola, amelynek csúcsa van azon a ponton.

Megjegyzés: Ez nem azt mondják, hogy a grafikon egy másodfokú függvény nevezzük parabola. Azt mondja, hogy a függvény grafikonját egy parabola. Ez azért van, mert egy ilyen görbe matematikai felfedezett és elnevezett a parabola előtt (a görög pi # 945; # 961; # 945; # 946; # 959; # 955; # 942; -. Az összehasonlítás, összehasonlítás, hasonlóság) a színpadra a részletes vizsgálat tulajdonságok és a másodfokú függvény grafikon.

Parabola - a metszésvonala egy köralakú kúpot egy sík nem halad át a csúcsát a kúp és a párhuzamos egyik alkotója ennek kúp.

Parabola van egy másik érdekes tulajdonsága, amely szintén használható, hiszen a definícióban.

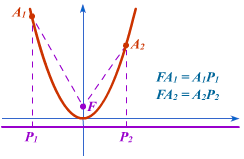
A parabola a pontok halmaza a síkban, amelynek távolsága a sík egy bizonyos ponton, az úgynevezett a hangsúly a parabola, a távolság azonos egy bizonyos egyenes vonal, az úgynevezett direktrixét egy parabola.

Szerkesszünk egy másodfokú függvény grafikonján, akkor vázlatot Keypoint.
Például, a függvény az y = x 2 pont veszi

De minden esetben a pontok épülhet csak egy vázlatot a grafikont a másodfokú függvény, azaz a egy hozzávetőleges menetrendet. Ki kell építeni a parabola pontosan, akkor kell használni a tulajdonságait: a fókuszt és direktrixét.
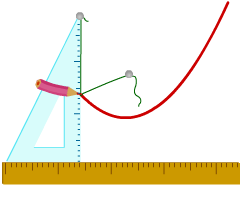
Fegyveres papír, vonalzó, derékszögben, két gombbal és egy erős cérnát. Csatolása egy gombot körülbelül a közepén egy papírlap - amit lesz a hangsúly a parabola. Második gomb, csatolja a tetején Az alsó sarokban a sokszög. Alapján gombok rögzítse menet úgy, hogy annak hossza megegyezik a gombok között nagy befogó gon. Rajzolj egy egyenest nem halad át a hangsúly a parabola a jövő - direktrixét a parabola. Csatolása a sort a igazgatónő, és a négyzet, hogy a vonal, mint az ábrán látható. Mozgassa a téren mentén uralkodó, miközben nyomja a tollat ​​a papírra, és a gon. Győződjön meg arról, hogy a cérna feküdt.

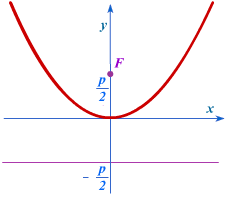
Mérje meg a távolságot a fókusz és az direktrix (emlékszik - közötti távolság a pont és a vonal által meghatározott függőleges). Ez a fokális paraméter a parabola p. A koordináta-rendszer látható a jobb oldali ábra, mi parabola egyenletnek formában: y = x 2 / 2P. Az én méretarány fordult függvény grafikonját az y = 0,15x 2.

Megjegyzés: Ahhoz, hogy egy adott parabola egy adott méretű, meg kell csinálni a dolgokat, de más sorrendben. Meg kell kezdeni a koordináta tengelyekkel. Majd rajzoljon egy igazgatónő, és meghatározza a helyzetét a hangsúly a parabola. És csak akkor tervezési eszköz a sokszög és a vonal. Például, építeni a kockás papírra egy parabola, amelynek egyenlete y = x 2 hangsúlyt kell helyezni, a parttól 0,5 sejtek direktrixét.

Tulajdonságok függvény az y = x 2

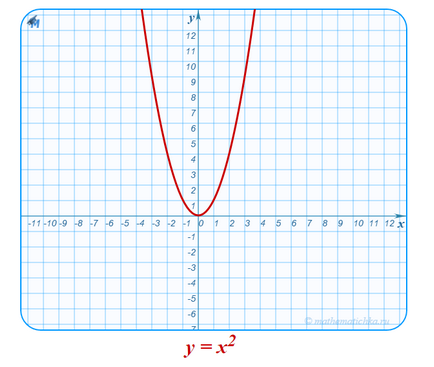
1. A domain a funkció - az egész szám sor: D (f) = R = (-∞; ∞).
2. Field függvény értékei - a pozitív félig: E (f) = [0; ∞).
3. A függvény az y = x 2 még: f (-x) = (-x) 2 = x 2 = f (x).
   Az y-tengely a szimmetriatengelye a parabola.
4. Az intervallum (-∞; 0) A függvény monoton csökken.
   A (0; + ∞) függvény monoton növekszik.
   
5. Azon a ponton, x = 0 elér egy minimális értéket.
   A pont koordinátái (0, 0) az a csúcsa a parabola.
6. A függvény folytonos a saját domain.
7. Aszimptota nem.
8. A nullákat: y = 0 x = 0.

A tulajdonságok egy kvadratikus függvény az általános formában.

1. A domain a funkció - az egész szám sor: D (f) = R = (-∞; ∞).
2. Tartományban a funkció függ a jele az együttható.
   Amikor a> 0 parabola ága felfelé, a függvény egy minimális (ymin), de nem rendelkezik a legnagyobb érték: E (f) = [ymin; ∞);
   egy 2 + bx + c se még nem furcsa.
   A szimmetria tengelye a parabola egy sor x = -B / 2a.
   A függvény lesz még csak abban az esetben, ha ez a vonal egybeesik a tengely Oy. azaz ha b = 0.
3. Amikor a> 0 monoton csökkenő függvény a intervallumon (-∞; -b / 2a) és monoton módon növeli az intervallum (-b / 2a; ∞).
   Egy 0 - minimum funkciót.

Mindkét érték képlettel definiált y = - b 2 - 4ac _______. 4a

A lényeg a csúcs koordinátáit a parabola.

A függvény folytonos a saját domain.

Aszimptota nem.

A parabola metszi az ordináta a ponton (0; c).
Ha szögletes trinomiális van deytsivtelnye gyökerek x1 ≠ x2. a parabola metszi az x tengely pontokon (x1, 0) és (x2; 0).
Ha X1 = X2 tekintetben abstsics parabola tengelye azon a ponton (x1; 0).

A származékot másodfokú függvény kiszámítása az alábbi képlet szerint (ax 2 + bx + c) „= 2ax + b.

A grafikon a másodfokú függvény által megadott általános képletű, a legjobb konstrukció és vizsgálat segítségével átalakítási szabályok grafikonok.
Ebből a célból, az egyik először át kell menni a képlet y = ax 2 + bx + c, hogy alkalmas formában transzformáció, y = m (kx + l) 2 + n. ahol k, I, m, n - amelyek száma függ a, b, c. azaz eszembe
.
Ezután vesszük a parabola y = x 2 és alkalmazza a következő átalakulás rá:

• Párhuzamos transzfer (shift) eredeti parabola l = b / 2a egységek balra (ha L 2 - 4ac) / 4a egységek felfelé vagy lefelé függően jele n (ha n> 0-ig).

A képleteket ilyen átmenet lehet betanult, de meg lehet tanulni, hogyan osztja a teljes négyzet egy háromtagú adott együtthatók. Ez a képesség nagyon hasznos is megoldására néhány egyenletek és egyenlőtlenségek, kiszámítható integrálok, stb

Vegyük ezt a példát:
Legyen y = 3x 2 - 5x + 2
1) össze zárójeles első két kifejezés, és vegye ki a zárójelben együttható x 2.
2) A zárójelben szaporodni, és osszuk el 2 egyidejű együttható x.
3) össze képlet binomiális építés egy négyzet: a szögletes zárójelek van belül x szám. kétszerese a termék x frakciója által 5/6. Ahhoz, hogy ezt a képletet hiányzik a második tér, így hozzá a hiányzó kifejezés 5 2/6 2 és vonjuk, hogy ugyanabban az időben, hogy megőrizze az eredeti kifejezés értéke.
4) Mi kapcsolja ki a tér, amelyet a képlet és nyilvánosságra nagy zárójelben.
5) A fennmaradó numerikus frakciókat bemutatni a közös nevező, és adja ki.

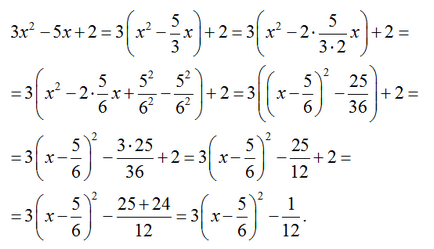
Tehát, hogy építsenek egy függvény grafikonját y = 3x 2 - 5x + 2 a gráf y = x 2 az, hogy az utolsó lépés a Ox tengely jobbra által 5/6 ≈ 0,83 egység. Ezután mentén húzódnak a Oy tengely 3-szor és végül csökkentette Oy tengelyen 1/12 ≈ 0,08 egység.
Nézd, mi történt.

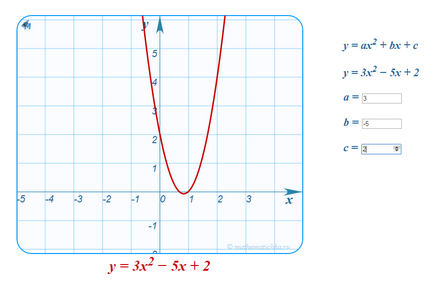
Ha egy tanítványom, vagy előfizető. akkor dolgozni interaktív változatai ezek grafikonok.

Feladat:
Construct a jellemző pontjait a grafikon vázlat y = x 2.
átalakítási eljárás kap egy vázlatot grafikon y = -x 2 + 4x + 6.
Nézd milyen rámutat a grafikon ennek a funkciónak metszi a tengelyt Ox és hasonlítsa össze a koordinátákat (az abszcissza) a gyökerek az egyenlet 2 -x + 4x + 6 = 0. által kiszámított diszkrimináns. Mennyire pontos a grafikus megoldás kiderült az egyenlet?

Mi átalakítsa a kifejezést a kibocsátás egy tökéletes négyzet:

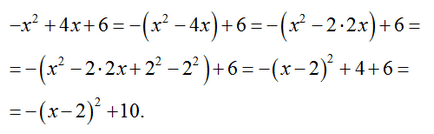
Épület egy függvény grafikonját
.

Ehhez használja a következő lépéseket: 2-sejtes jobbra eltolási, kapcsolja le ágak (csúcs - egy pont, amelyhez képest a forgócsapos), emelje fel a felső és a, illetve a teljes parabola legfeljebb 10 sejtek. Itt van, amit meg kellett volna

.

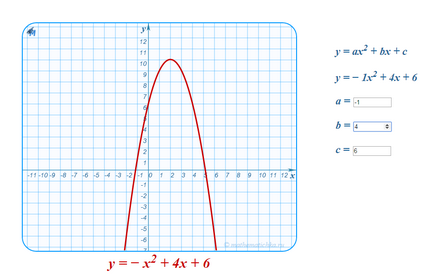
Vizuálisan meg a gyökereket. Parabola metszi Ox tengely mintegy egyötöde a sejtek balra mínusz egy és azonos jogokat az öt, azaz x1 ≈ -1,2. x2 ≈ 5,2.

A megoldás szerint a képletek a megállapítás a gyökerek egy másodfokú egyenlet ad választ x1 = 2 - √10 __. x2 = 2 + √10 __.
A kalkulátor számítási x1 = -1,162277660. x2 = 5,162277660.

Parabola - nagyon érdekes görbe másodfokú függvényt gyakran megtalálható a leírása a különböző természeti jelenségek, a gazdasági folyamatokat.

A grafikonok a másodfokú függvények és az együtthatók a másodfokú trinomiális.

A pozíció és formája a parabola a jel szerint, és értéke az együttható és - együttható x 2.

A pozíció és formája a parabola a jel szerint, és a értéke együttható b - együttható x.

A pozíció és formája a parabola a jel szerint, és a paraméter értéke c.

Kihívások az elemzés a grafikon egy másodfokú függvény.

Feladatokat, mint a „Set közötti levelezés együtthatók négyzetes trinomiális és A grafikonok a másodfokú függvények” találhatók JEG matematikai kilencedik évfolyam, valamint hogy szükség van a lemondására vizsga évfolyam 11 közbenső lépéseket.