magassága a háromszög, orthocenter
A távolság a háromszög csúcsa és az ellenkező oldalon az úgynevezett magassága. Formálisan, ez a legrövidebb közötti intervallum a háromszög csúcsa és (hosszabbítás lehetséges) az ellenkező oldalon.
Minden háromszög magassága 3, hogy metszik egymást egy pontban - orthocenter. Ha használjuk a szabványos jelölés, az ABC háromszögben. Három magasságban: ha. BHB. CHc. Ez a három szegmens metszik egymást egy pontban - orthocenter (H-pont az ábrán) a háromszög. A tompaszögű háromszög (amelynek egy szöge nagyobb, mint 90 °), a orthocenter háromszögön kívül.
A magassága akut háromszög
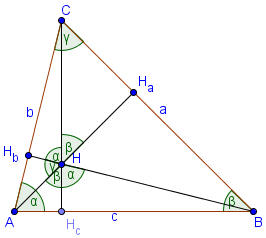
Orthocenter - egy pont belsejében egy háromszöget.
∠ AHB = 180 - γ = α + β
∠ BHC = 180 - α = β + γ
∠ AHC = 180 - β = α + γ
∠ AHHc = β, ∠ BHHc = α, ∠ BHHa = γ
Magasság tompaszögű háromszög
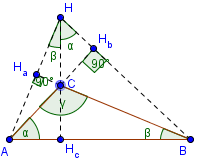
Orthocenter ki treugolnka.
Két magasságban és mindig kívül esnek a háromszög.
∠ AHHc = ∠ CBA = β
∠ Hc HB = ∠ CAB = α
derékszögű háromszög
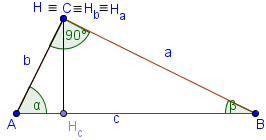
AHa magassága egybeesik AC.
Ez egybeesik a magassága BHB BC.
Orthocenter H egybeesik C.
∠ Achc = β, ∠ BCHc = α
R - a sugara a körülírt
r - a sugara a beírt kör
p - poluperimert: (a + b + c) / 2