Lineáris, kvadratikus, és a teljesítmény a funkció megoldások példák
A grafikon az eredeti funkció egy parabola. Mivel egyenlet

kényelmes használni koordinátáit két metszéspontja egy parabola az abszcissza tengely és a koordinátákat a csúcsa a parabola.
Találunk gyökerei a másodfokú egyenlet. Ezek azok az értékek,

Így, a metszéspont az abszcisszával

Az abszcissza a parabola csúcsa félúton található metszéspontja a tengelye a parabola

Következésképpen, az értéke az abszcissza a parabola csúcs:

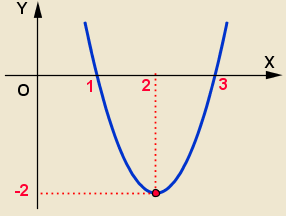
Behelyettesítve az értéket a függvénykifejezést találunk ordináta csúcsa a parabola:

Így a csúcsa a parabola az a pont

Az így kapott három pontot mi a telek parabola.
megjegyzés:
Amikor az épület gyakran használják grafikus metszéspontja az y tengelyen. Erre a kezdeti érték helyettesített egyenlet


A grafikon a másodfokú függvény felhasználásával konstruálható elemi transzformációk a grafikon

Ebben az esetben az átalakulás az alábbi lépéseket.