Lineáris algebra mátrix

Az inverz mátrixot 13

Helyezett 16

Lineáris függetlenség 21

Egy lineáris egyenletrendszer 24

Módszerek megoldására rendszerek lineáris egyenletek 27

27, az inverz mátrix módszer

Eljárás megoldására rendszerek lineáris egyenletek négyzetes mátrix a Cramer szabály 29

Gauss módszer (eljárás egymást követő megszüntetése változók) 31

Razmeramhn- mátrix egy téglalap alakú asztal a számok, soderzhaschayamstrok instolbtsov. A számok teszik ki a tömb, az úgynevezett mátrix elemeinek.

Mátrixok általában jelöljük tőke latin betűkkel, és elemek - ugyanaz, de kisbetűvel kettős indexálás.

Vegyük például a mátrix a dimenzió 2 x 3:

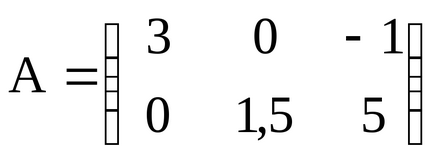
Ebben a mátrixban a két sor (m = 2), és három oszlopot (n = 3), azaz a Ez áll a hat elementovaij. gdei- sorszám, J - száma az oszlop. Ebben az esetben tart értékek 1-2 és egy-három (rögzített

). Nevezetesen, a11 = 3; A12 = 0; A13 = -1; A21 = 0; A22 = 1,5; A23 = 5.

A mátrixok A és B jelentése azonos méretű (M x N) nazyvayutravnymi. ha azok azonosak elemenként, t.e.aij = bij számára

, azaz A lyubyhiij (tud zapisati, j).

Mátrix-karakterlánc - álló mátrixot egy sor, oszlop amatritsa - álló mátrixot egy oszlop.

Például, - egy mátrix sor, és

.

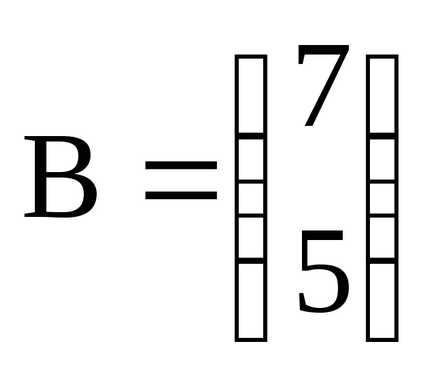
Négyzetes mátrix n-ed rendű - egy mátrixot, egy számot, ahány a sorok és oszlopok egyenlő n.

Például,

- másodrendű négyzetes mátrix.

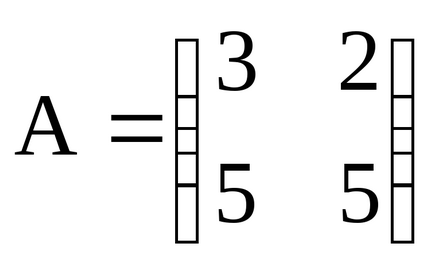
A diagonális mátrix elemeinek - az elemek, amelyeknek sorban a szám egyenlő a számát az oszlop (aij, i = j). Ezek az elemek obrazuyutglavnuyu diagonális mátrix. Az előző példában, a fő diagonális formájában elementya11 = 3 5 = ia22.

A diagonális mátrix - egy négyzetes mátrix, amelyben az összes off-átlós elemek nullával egyenlő. Például,

- diagonális mátrix a harmadik rend. Ha minden az átlós elemek egyenlő eggyel, akkor a mátrix nazyvaetsyaedinichnoy (általában betűvel jelöljük E). Például,- harmadik rendű egység mátrix.

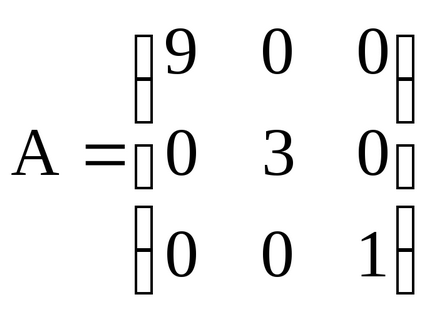
A mátrixot az úgynevezett nulla. ha minden elem nulla.

A négyzetes mátrix az úgynevezett háromszög alakú. ha minden elem alatt (vagy felett) a fő diagonális nullával egyenlő. Például,

- háromszögmátrix a harmadik rend.

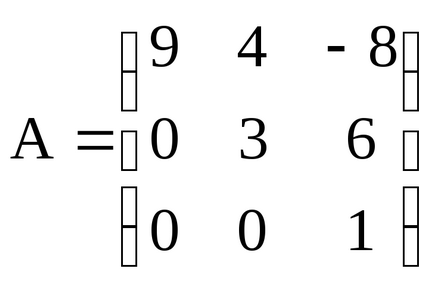
manipulálása mátrixok

A mátrixok hajtsa végre a következő műveleteket:

1. Szorzás egy mátrix egy szám. A termék A mátrix a B mátrix = chislonazyvaetsya A elemek kotoroybij = aij számára lyubyhiij.

Például, ha

, az.

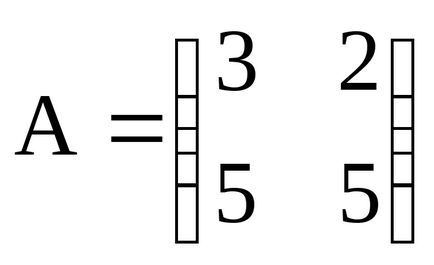
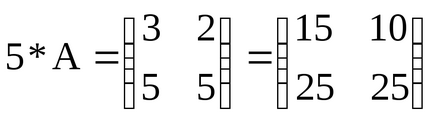
2. mátrixok összeadása. A összeg két A és B mátrix azonos méretű m x n a C mátrix = A + B, amelynek az elemei Sij = aij + bij dlyai, j.

Például, ha

az

.

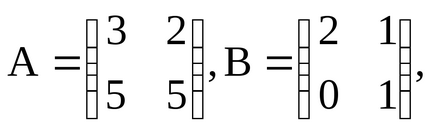
Megjegyezzük, hogy az előző művelet lehet meghatározni kivonás mátrixok azonos méretű: a különbség az A-B = A + (-1) * B.

3. Szorzás mátrixok. A termék A mátrix razmeramxnna razmeranxpnazyvaetsya mátrix B jelentése C mátrix minden eleme Sij összegével egyenlő a termékek elemek i-edik sorának az A mátrix megfelelő elementyj-edik oszlopa a B mátrix, azaz ..

, a mátrix termék mérete 2 x 3, és ez lesz a formában:

Ebben az esetben, az A mátrix koherens a mátrix W.

Ennek alapján a művelet a szorzás a tér mátrixok meghatározott hatványozást működését. Egy bizonyos fokú pozitív egész szám m (m> 1) a négyzetes mátrix m mátrixok a termék egyenlő A, azaz a

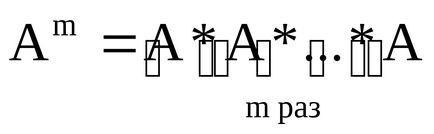
Hangsúlyozzuk, hogy a túl (kivonás) és szaporodása mátrixok nincs definiálva bármely két mátrixot, de csak, hogy megfeleljen a speciális követelményeket a dimenziója. Megtalálására összege vagy különbsége a mátrix méretének meg kell egyeznie. Ahhoz, hogy megtalálja az oszlopok száma a mátrix termék az első közülük meg kell egyeznie a száma a második sorban (mint koherens mátrix nevezik).

Vegyünk néhány műveletek tulajdonságainak analóg a tulajdonságait műveletek számát.

1) kommutatív (kommutatív) hozzáadásával jog:

2) asszociatív (asszociatív) joga továbbá:

(A + B) + C = A + (B + C)

3) Az elosztó (elosztó) a törvény felett szorzás továbbá:

5) asszociatív (asszociatív) szorzás jog:

Kiemeljük, hogy a kommutatív törvény szorzata mátrixok általában nem teljesül, azaz, AB BA. Ezen túlmenően, a létezését a AB nem feltétlenül jelenti a létezését VA (a mátrix nem lehet konzisztens, majd a terméket általában nem határoztuk meg, mint a fenti példában a mátrix szorzás). De még ha a két termék nem létezik, ezek általában különböző.

Abban a különleges esetben, kommutatív törvény termék vagy egy négyzetes mátrix által az identitás mátrix az ugyanabban a sorrendben, és ez a termék egyenlő egy (az identitás mátrix szorzás hasonló megszorozzuk egységet, ha a szorzás számok):

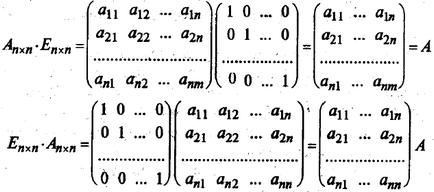
Hangsúlyozzuk másik különbség mátrixszorzással származó szorzás a számok. A termék a számok lehet nulla akkor, ha legalább egyikük értéke nulla. A mátrixok lehet mondani, hogy termék nem nulla mátrix lehet nulla mátrixba. Például,

Mi továbbra is vizsgálja mátrix műveletek.

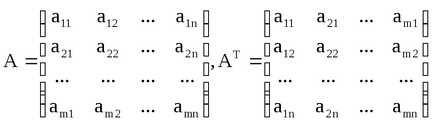
4. Átültetés mátrix egy olyan művelet, átmenet a mátrix T A razmeramxnk razmeranxm mátrixot, amelyben a sorok és oszlopok cserélték:

%.

Tulajdonságok átültetés művelet:

1) A meghatározást az következik, hogy ha a mátrix átültetés kétszer, visszatérünk az eredeti mátrix: (A T) T = A.

2) A konstans faktor lehet venni kívül átültetés (A) ​​T = T A.

3) Átültetés elosztó tekintetében hozzáadásával és szaporodását mátrixok: (AB) T = B T A T és (A + B) T = B T + A T.