Lecke - szinusz és koszinusz az összeg az érvek

Rövid leírása a dokumentum:

Ennek során a tanuló trigonometria a tanulók, akik ki vannak téve a funkciókat az alapvető tulajdonságait, viselkedését a karaktert. Ezek közül a legfontosabb funkciók periodikus függvények a szinusz, koszinusz, tangens és kotangens. Ezek a különböző időszakokban és előírásoknak.

A diákok megtanulták, hogy felépítse a grafikonok és adatok elemzése funkciók. Vizsgált domain, domain értékek, növekvő és csökkenő hiányosságok és m. P.

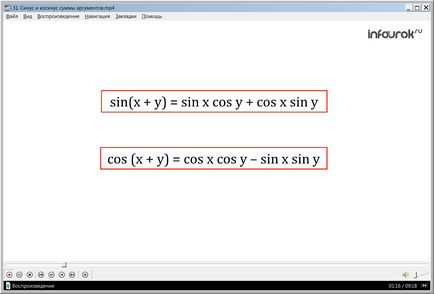
Az egyik alapvető alapvető képlet az összeg a szinusz és koszinusz az összeget, amelyet gyakran használnak különböző problémák megoldásában. Amikor házi feladatot, vagy a különböző független és ellenőrzési munkák a diákok minden bizonnyal szembe kell néznie azzal, hogy használja a képlet adatokat. Ezért fontos, hogy jól megértsük ezt a leckét, hogy jobban és hosszabb ideig emlékezni.

ezek a képletek vannak bekarikázva piros doboz, ezzel is hangsúlyozva annak fontosságát emlékezés bemutatásra kerül az első része a bemutatót. Látjuk, hogy ezek eltérnek egymástól. Ne feledje, a képlet nem lesz nehéz, ha megfelelően alkalmazzák a gyakorlatban.

A bemondó elmagyarázta a diákoknak, hogyan szeretné olvasni ezeket a képleteket helyesen. Egyes tanárok megkövetelik diákok játszani a verbális formában ezek a képletek a célja egy matematikai nyelvet. Tehát meg kell gondosan hallgatni a hangszóró, és rögzíti azt, ha szükséges egy notebook.

Követve az első gyakorlati példát. Meg akarja találni a szinusz 105 fok. Hangszóró megoldást kínál erre például eredményt szögben 105 fokos összegeként két szög, azaz 45 és 60, szinusz és koszinusz amely a diákok tudják, és emlékezett arra, hogy a címzettje táblázat értékeinek trigonometrikus függvények.

Ezek a táblázatok céljára emlékeztetők jelennek meg. A kiemelt értékek, hogy szükségünk van. Továbbá arra képletű mennyiségű sine érv, mellyel a megoldására további példát. Az utolsó szakaszban meghatározott értéket behelyettesítjük a táblázatban, és a választ kapunk.

A második példa azt javasolja, hogy egyszerűsítsék egy komplex expressziós tartalmazó trigonometrikus függvények. Hogy oldja meg a problémát mindkét képlet korábban tárgyalt. Az oldatot bizonyított lépésről lépésre. Hogy a diákok megértsék, ahol az értékek jelennek meg a táblázatban a trigonometrikus értékek és kiemeli az alkalmazott sejtek.

Ennek eredményeként, mint az előző példában, a válasz megjelenik.

A harmadik példa hasonló az első, a negyedik és az adott tovább a döntés sokkal bonyolultabb és érdekesebb. Meg kell találni a koszinusza összege az érv, ha tudjuk, az adatok egy részét. Előnyösen úgy a problémát a tanár vagy tutor. Amennyiben a tanuló okos és jó matematikai keret, akkor képes lesz arra, hogy megértsék és egymástól függetlenül, ha az elmulasztott leckét, vagy szeretné visszaállítani a memóriában. Annak érdekében, hogy megszilárdítsa az megértsük ezeket a példákat, akkor a diákok néhány más hasonló példa a tankönyv, amelynek megoldása akkor kell használni a képlet szinusz és koszinusz összege az érveket.

Az ötödik példa a komplexitás az első helyet foglalja. Azt javasolja, hogy megoldja trigonometrikus egyenletek, amelyeket meg kell jó emlékezni és megérteni, hogyan használjuk a trigonometrikus képletek.

A döntés nagyon világos és részletes. A bemondó magyarázza az egyes lépéseket, ne hagyjon ki egyetlen fontos pillanatot. A jobb oldalon a megoldásokat tartalmazott buborékokat és képletek, amelyek alkalmazzák, amikor a munkát elvégezni.

Mi már ismerik a trigonometrikus függvények, grafikonok, megtanulták, hogy megoldja a trigonometrikus egyenletek. És most folytassa a tanulmány a trigonometrikus képletek amelyhez átalakítani trigonometrikus kifejezések.

Ezek közül a legfontosabbak a trigonometrikus formula, közkeletű nevén az összege szinusz és koszinusz az összeget.

sin (x + y) = sin x cos y + cos x sin y,

cos (x + y) = cos x cos y - sin x sin y.

Ezek az egyenletek is olvasható, az összeg két szinusz szög egyenlő a termék közötti szinusz és koszinusz a szög az első szög és a második termék a sinus és cosinus az első kanyarban a második szög;

koszinusza összege két szög egyenlő a különbség a termék a koszinusz ezen szögek, és a terméket az összeg ezen szögek.

Ezekből képletek tudjuk levezetni szinte az összes képlet trigonometria.

Hogyan kell használni ugyanazt a formulát összege szinusz és koszinusz az összeget. Tekintsük a példák, hogy minden képlet lehet alkalmazni, mint a „bal” és „jobb”.

Példa 1. Compute sin 105 °.

Határozat. Ábrázoljuk Százöt fok, mint az összege 105 ° = 45 ° + 60 °. Tudjuk, hogy a bűn, 45 ° = cos 45 ° =. sin 60 ° =. cos 60 ° =.

Mutasd a táblázatot az értékek

Behelyettesítve ezeket az értékeket a képlet összege sine

sin (x + y) = sin x cos y + cos x sin y,

Togdasin 105 ° = sin (45 ° + 60 °) = sin 45 ° cos 60 ° + cos 45 ° sin 60 ° = ∙ + ∙ = =.

(Száz és öt fok szinusz sine összegének negyvenöt fokos és hatvan fok, és egyenlő az ezt az összeget frakció, a számláló, amelynek a gyökere a kettő összege, és a gyökér a hat, és a nevező - négy.)

Válasz: sin 105 ° =.

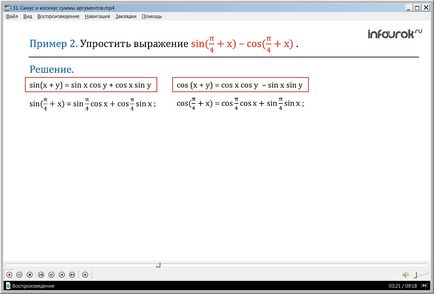
Példa 2. egyszerűsítik a kifejezés sin (+ x) - cos (+ x) (a különbség sine pi osztva négy, plusz X, és a koszinusza pi osztva négy, plusz X).

Határozat. Alkalmazzuk a szinusz képletet a csökkentett mennyiségű sin (+ x)

sin (x + y) = sin x cos y + cos x sin y,

Majd csökkentse sin (+ x) = sin + cos cosh Sinh.

Alkalmazzuk a képletet az összeg a koszinusz kivonandó cos (+ x)

cos (x + y) = cos x cos y - sin x sin y.

Kivonandó cos (+ x) = cos + sin cosh sinh

sin (+ x) - cos (+ x) = sin cos x + cos sin x - cos cos + sin sin x x

Mutasd a táblázatot az értékek

A táblázatban található értékek találni az értéket a bűn és a cos

sin = cos = helyettesítse ezeket az értékeket a kifejezést, és megszerezni:

= ∙ + ∙ cosh sinh - ∙ + ∙ cosh sinh

Cosh ∙ - ∙ = 0 cosh, Sinh van ∙ + ∙ Sinh amely 2 ∙ ∙ Sinh Sinh get.

sin (+ x) - cos (+ x) = sin cos x + cos sin x - cos cos + sin sin x = x

= ∙ cos x + ∙ sin x - ∙ cos x + ∙ sin x = 2 ∙ ∙ sin x = sin x. Ez egy teljes numerikus megoldása.

A válasz: sin (+ x) - cos (+ x) = Sinh.

Példa 3. Számítsuk sin 17 ° cos 13 ° + cos17 ° sin 13 °. (Sine Tizenhét fok, szorozva a koszinusz a tizenhárom fokkal koszinusza Tizenhét fok, szorozva a szinusz a tizenhárom fok).

Határozat. Ez a kifejezés lehet „dobni” a összege érvek sine 17 ° és 13 ° (azaz. A „jobbról balra” sine képlet az összeg).

sin (x + y) = sin x cos y + cos x sin y,

sin cos 13 ° + cos sin 13 ° = sin (+ 13 °) = sin 30 ° = (összege a termék a szinusz tizenhét fok koszinusza tizenhárom fok és dolgozik koszinusz tizenhét fok sine tizenhárom fok egyenlő a szinusz összege tizenhét és tizenhárom fok egyenlő a szinusz harminc fok egyenlő egy második).

4. példa Számítsuk cos (x + y), ha tudjuk, hogy cos x = y = cos

0 X (x nagyobb, mint nulla és kisebb, mint két PI) a 2p (y pi több mint három a két, de kevesebb, mint két pi).

Határozat. Az általunk használt formula a koszinusz összege:

cos (x + y) = cos x cos y - sin x sin y.

Értékek cosx és kényelmes szett. Kiszámoljuk az értékek és sinx siny. Mi az alapvető, trigonometrikus azonosság: sin 2 t + cos 2 t = 1. Van: sin 2 x = 1 - cos 2 x. és x = cos. akkor helyettesítő képletű és szerezzen = 1 - () 2 = 1 - =.

sin 2 x = 1 - cos 2 x = 1 - = Ez a numerikus teljes megoldást.

Azzal a feltétellel, az X érv tartozik az első negyedévben, és ez a szinusz pozitív. Ezért sinh =.

Hasonlóképpen, sin 2 y = 1 - cos 2 y = 1 - =. de az érvelés y tartozik a negyedik negyedévben, és ez sine negatív, így a sin y = -.

Behelyettesítve a kapott értékeket, és a készítmény összetételében megadott összegére a koszinusz kapjuk cos (x + y) = ∙ - ∙ = + = 1.

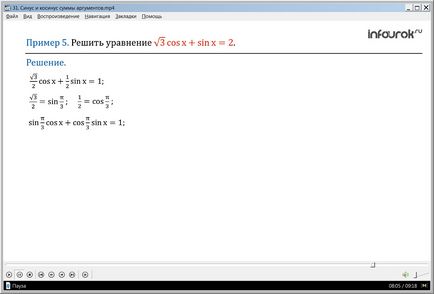
5. példa megoldásához egyenletet cosx + sinx = 2.

Osszuk mindkét oldalán két, megkapjuk cosx + sinx = 1

Itt egyenlet formájában képlet sine összeg két szög:

és emlékszem, hogy = sin. a = cos.

Mutasd a táblázatot az értékek

cos x + sin x = 1,

SinCos x + cos sin x = 1,

Ezután a bal oldali az egyenlet jobb oldalán a képlet összege szinusz és x érveket. Így a bal oldali részén a kifejezés egyenlő sin (+ x)

Mi vagyunk a megállapítás az x értékét