Kiszámítása származékok
Mottó: Egy megkérdezte: „Mi a származék különbözik a terméket?” A „származékok tanul az osztályban a matematika, és a terméket - a leckét irodalom” -, majd a hallgató választ.
A mottó le a valós helyzetet a praxisomban. Felmerült a kérdés, ha a tanuló kusza szabályok differenciáló, különösen, hogy nem tudja meghatározni a származtatott termékek két funkciója van. Annak érdekében, hogy ez az értelmezés ezt a cikket, hogy emlékeztessem önöket, hogy teszünk csak a matematika, és itt a „termék” kifejezés azt jelenti, hogy a szorzás eredményét, és a „származék” a határa az arány a növekmény funkció a növekmény az érvelés, ha az utóbbi nullához. A számítás a folyamatot nevezik differenciálódás származékot.
Származékai elemi függvények definíció szerint, azaz a határérték kiszámítása csak egyszer, egy előadás (az osztályban), hogy biztosítsa a kapcsolatot, és határérték-származék. A jövőben csak a gyakorlati alkalmazás ezt a koncepciót, így kiszámítható a származék kész képletek és szabályok differenciálódását funkciókat.
Itt nézd meg, hogyan kell és hogyan nem, hogy kiszámolja a származékok, de sajnos, sok diák és még a diákok csinálnak.
Hogyan számoljuk ki származékok
Meg van írva mindenhol, a tankönyvek és a különböző helyszínek a hálózatban.Ahhoz, hogy megtalálja-származékok, szükséges, hogy egy vagy más forrásból, még tanulni Formula differenciálódását elemi függvények. Például, egy részletes cikket a táblázat a származékok és primitívek. Bonyolultabb, mint táblázatos, ezek együttes működése a szabályok számítási származék az összeg, a termék, a frakció. A megfelelő matematikai kifejezések, mint akkor sehol. De véleményem szerint, a szabályok a differenciálás a feladatok jobb meghatározása és memorizálni a szavakat:
- A konstans tényező lehet venni, mint egy jel a származék.
- Származékát az összegével megegyező összeget a származékok.
- A származék terméket egyenlő „származék az első tényező megszorozva a második derivált, plusz a második tényező szorozva az első”.
- A származék a frakció egyenlő „egy származéka, a számláló szorozva a nevező, mínusz a származék a nevező, szorozva a számlálót osztva a nevező a téren.”
- A származék az összetett függvény az a származék, a külső funkciót, szorozva a származékot a belső, és a kiszámított „folytatása” az asztalra.
Hogy, hogy nem számít származékok
- Először is, nem szükséges, hogy bonyolítja az egyszerű.
- Ne tévesszük össze a feltételeket és tényezőket (összeg és a termék).
- Ne tévesszük össze power-Xa és az exponenciális függvény fejszét.
- Nem szabad elfelejteni, hogy a származék egy összetett függvény kiértékelése „folytatása”, amíg a táblázatos formula.
- Ne légy félénk, hogy zárójelbe.
A legtöbb a következő példákkal szemléltetjük a számítási-származékokat, amelyek
1. A számítások nagyon rosszul. nyilvánvaló hibák;
2. Az igaz, de nem optimális. azaz hosszú, és valószínű hiba a figyelmetlenség;
3. elég jól.
Megjegyzés a szabály, hogy feltettem az első számú.
Ha a munka az egyik tényező állandó, akkor nem szükséges, hogy a szabály az átdolgozást. Sőt, nem szükséges, hogy ezt azért, mert gyakran kíséri egy ilyen művelet hiba. A konstans tényező lehet venni, mint egy jel a származék!
Ha egy töredéke a számláló vagy a nevező állandó, akkor nem szükséges, hogy használja a szabály-származék frakciókat. Ez az intézkedés a tanulók gyakrabban kíséri hibákat. A konstans tényező lehet venni, mint egy jel a származék!
A leggyakoribb hiba a következő példákban - elfelejteni, hogy a bar (kijelölésére vonatkozó származék) a száma, illetve, hogy tegye, és a „nem látja” a következő hatás, azaz a nem veszi figyelembe, hogy a származék konstans (szám) egyenlő nullával.
Itt, az első és a harmadik példa az egyszerűség és a minőség a megközelítés a zárójelben c bevezetését numerikus tényezővel nyilvánvaló. De ez nem annyira egyértelmű, a második például, ahol a nevező trigonometrikus függvény. Továbbá egyetértek, hogy azokat a fiatalokat, akik rendelkeznek rossz származékot komplex funkció (szabály 5), még előnyösebb ebben a példában lehet a szabály differenciálás frakciót.
Azonban számos egyéb funkció, különösen az energia, csak meg kell nevező „fordulat” a számlálóban, és a gyökerek - részben azért, mert ebben az esetben tudjuk használni a legegyszerűbb és a leginkább emlékezetes táblázatos (x # 945; ) = # 945; X # 945; - 1.
Ebben a két példában, bemutatva a szokásos hibákat a differenciálódás a frakció egy állandó, és a következő példában, az átmenet a gyökér a frakcionált teljesítményre van szükség, mert különben gyakran elfelejtett hogy egy ilyen funkció nem egy asztal és differenciálni kell a szabály alapján az összetett funkciók.
Állandó távú differenciálás nullázni konstans tényező a differenciálás megmarad.
Továbbá, valamilyen oknál fogva, sok tanuló függvény deriváltját y = x 2 + 0,1 könnyebb kiszámítására, mint az azonos típusú származékot (0,1 + x 2)”. És a függvény deriváltját y = 0,1 × 2 gyakran észre a létezését az első szabály, és a (x 2 x 0,1) „nincs.
Amikor, hogy ez a fajta hibát, ne feledje, hogy a permutáció összeg nem változik, és a permutációs tényezők nem változtatja meg a termék. Átrendezheti őket, ahogy tetszik, és óvatosan kell alkalmazni az első vagy a második levezetési szabályok.
Az első esetben, a változó a mértéke alapján, azt olvassuk: „X, hogy a hatalom a”. A második - egy változó a kitevő, ezt olvassuk: „és a hatalom X”. Jellemzők különböző képletek kiszámításához származékok különböző. Cm. Táblázat.
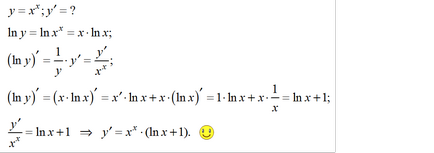
Ez egy komplex függvény, amely közvetlenül nem kapcsolódik semmilyen osztály hatalma, sem egy osztály bemutató. Kiszámítani a származékot az ilyen esetekben gyakran előállításához szükséges előzetes átalakítás. Például, az első kifejezés a logaritmusa, akkor figyelembe a származékok mindkét oldalán annak változók, és végül elérte egy egyenletet megtalálására a kívánt származékot az x változó.
Komplex függvény, ez a funkció nem függ közvetlenül a változóhoz, és a többi funkciót. Más szóval, az értéke nem lehet kiszámítani egy lépésben. Például, a függvény az y = sinx2 és y = sin 2 x összetettek. Lássuk, hogyan ezek kiszámítása, például akkor, ha x = 2.
Egy függvény az y = sinx2 először be kell emelt négyzet x 2 2 = 4, majd kiszámításához a szinusz értéke 4-dx. Mi ez egy számológép: sin4 = -0,75680249530792825. ≈ -0,76 (ne felejtsük el, hogy a trigonometrikus függvények érvek minősülnek radiánban).
Egy függvény az y = sin 2 x, először meghatározzák a szinusz 2-a számológép: sin2 = 0,9092974268256816. majd felálló az értéket a négyzeten sin 2 2 = (,9092974268256816.) 2 = ,82682181043180595. ≈ 0,83.
Így először az A értékét a belső működését és utána azt érvként, hogy a külső.
Az ötödik szabály differenciálás, a meghatározó származék kell tennie az ellenkezőjét - az első kiszámításához származéka külső függvény az érvelését, majd szorozza meg a származék a belsejében.
Mint már említettem, a leggyakrabban elkövetett hibák ezt a műveletet. Hibák nagyon eltérő lehet, a következő három közös.
1. hiba) Nem lehet csak alkalmazni a megfelelő szabályt, „nem megjegyezve, hogy” a komplex függvény.
A következő képlet, és az erő a differenciálódás trigonometrikus függvények használt nem szekvenciálisan, de egyidejűleg, származék helytelenül számított egy lépésben.
2. hiba) nem tudja kitalálni, ahol a külső és belső funkciók hol.
A következő példában, a kitevő a fenti x. azaz a fenti érv, tehát a mértéke a funkciója a belső és külső sinus. Tanítványa volt egyébként, úgy döntöttem, hogy a szinusz-négyzet és hibázott.
Ahhoz, hogy megszabaduljon az ilyen hibákat, megtanulják, hogy elemezzék összetett funkció külön belsejét és a külsejét, akkor csak meg kell nézni, hogy milyen sorrendben, hogy elvégzett számítások, és a differenciálás fordított sorrendben. Lehetőség van, hogy gondoskodjon a hiányzó zárójel, és ha továbbra is nehézségei, hogy további jelölést. Ami a fokozatot, akkor emlékezzen erre - miként a kijelölés áll kitevő, azaz az alap (emeljük).
12. példa.
A felhasznált végén a trigonometrikus szinusz a kettős szög formula, annak érdekében, hogy rögzítse a választ, hogy a legtöbb kompakt formában.
13. példa.
Itt a vége a tényezők is átrendeződik, hogy írni a választ tömörebb és olvasható formában.
Harmadik hiba) A szabály nem használják végéig
Amint azt figyelembe véve, hogy a funkció összetett és elegendő. És ha a funkció be van ágyazva többször is? Például a négyzetgyöke összegével logaritmusainak két különböző bázisok, amelyek közül az attól függ, hogy sinx. és a második cosx. Vagy az arkusz tangens függően természetes logaritmus, hogy van, viszont attól függ, hogy az x négyzeten.
14. példa.
15. példa.
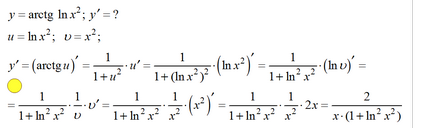
Az előző példa bemutatja a kiutat bevezetésével további szimbólumok. De véleményem szerint, ez még mindig nem a legjobb módja a hosszas számításokat. A legjobb megközelítés differenciálása összetett funkció - zárójelben, ami építhetünk egyértelműen, vagy legalább erősíteni a készség elképzelni mentálisan.
Mi megszervezzük a konzolok és fokozatosan felfedik kívül van. A tartalma a következő zárójelben változó felett a származtatás általános képletű fu „· (u)”. Származtatott fu „deriválhat az asztal helyett a képlet x u. Ha helyesen tette, a folyamat véget ér az a tény, hogy a tartalmát az utóbbi, a legbelső zárójelben teljesen egybeesik az egyik táblázat képletek a származékok.
