Kihívások a geometriai bizonyíték a tényeket a DPA

Azt javaslom, ezúttal, hogy gondoskodjon valami hasonló „bizonyíték-maraton”, hogy a kihívásokra, amelyek kínálják a változatok DPA kilencedik osztályosok matematika. Ezek a kapcsolódó bizonyíték egyszerű, de ugyanakkor nagyon hasznos geometriai tényeket. A cikk szándékosan nem adott részletes problémák megoldására, csak néhány vázlatot és tippeket. Próbálja meg legyőzni a maratoni egyedül, hiba nélkül és egy menetben.

Probléma 1. Igazoljuk, hogy a függőleges felezővonal szomszédos szögek.

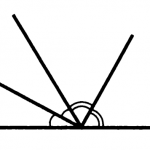
Szög α jelöli egy ív, β - két

Probléma 2. Két szegmens az AC és BD pontban metszik egymást, hogy a felezőpontja O. minden. Bizonyítsuk egyenlőség ACD és CAB háromszögek.

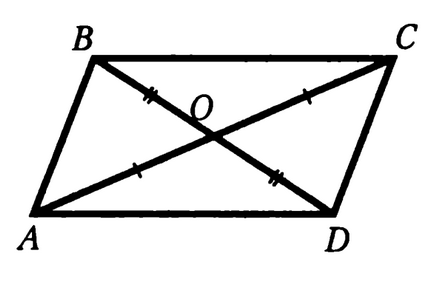
Az ABCD természetesen egy paralelogramma, de amennyiben ezt nem adják

Bizonyítás: háromszögek egyenlő mindkét oldalon, és a köztük lévő szög (BO = OD - azzal a feltétellel, AO = OC - feltétel, ∠DOC = ∠AOB - függőleges), azaz ∠ACD = ∠CAB. és mert hazudik keresztben közvetlen AB. CD és osztott AC. majd AB párhuzamos DC. Hasonlóképpen bebizonyítjuk párhuzamos vonalak BC és az AD. Tehát ABCD - paralelogramma definíció szerint. BC = AD. AB = CD (a paralelogramma szemközti oldalai egyenlő), AC - teljes az ACD és CAB háromszögek. így azok egyenlő három oldalról. QED.

Probléma 3. megjelenítése, hogy a súlyvonal a bázis egy egyenlő szárú háromszög, a felezővonal a szög a szemközti hordozótól, és merőleges az alapra.

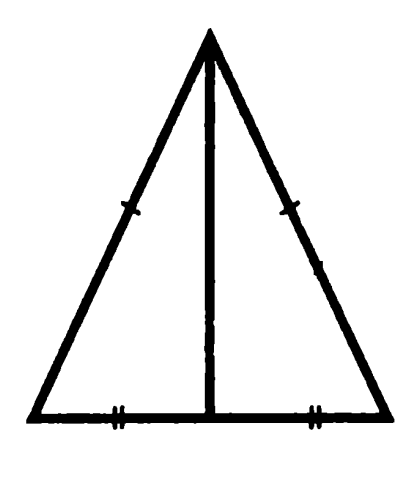
Által bezárt szögek a medián és a bázis, az úgynevezett „alsó”, a középértéket és oldalfelületein - „felső”

Bizonyítás: oldalirányú háromszögek az ábrán három oldalról, ahonnan a egyenlőség, első, „felső” szögek (kimutatták, hogy a felezővonal), másrészt, „alsó” szögek, hogy az összeg, mint a szomszédos, és 0-val egyenlő 180 azonban minden 90 0 (látható merőlegesség). QED.

Probléma 4. Bizonyítsuk be, hogy a medián végre, hogy az oldalán egy egyenlő szárú háromszög egyenlő.

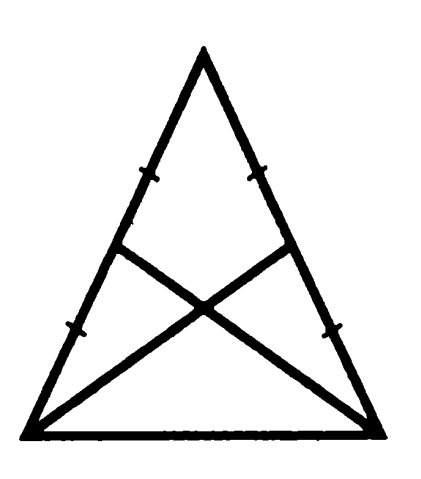
Háromszögek képződött medián, bázis és alsó fele az eredeti háromszög oldalai, az úgynevezett „alsó”

Bizonyítás: A szögek a bázis egy egyenlő szárú háromszög egyenlő, így a „rövid szénláncú” háromszögek egyenlő mindkét oldalon, és a köztük lévő szög, ami azt jelenti, az egyenlőség tartott mediánok. QED.

Probléma 5. Igazoljuk, hogy a szögfelező levonni a tetején a bázis egy egyenlő szárú háromszög egyenlő.

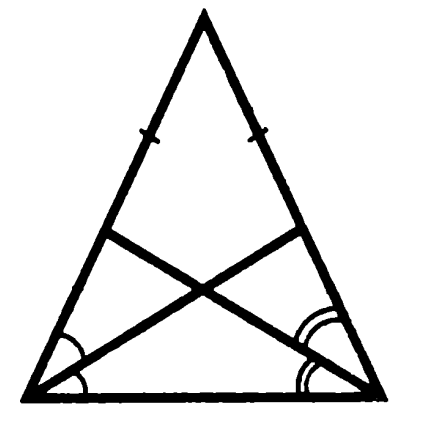
Minden jelölt szögek a képen, persze, egyenlő, bár, és vannak jelölve ívek

Bizonyítás: „alsó” háromszög egyenlő szárú, az alábbiak szerint a egyenlőség a szögek az alján, „oldalsó” háromszögek egyenlő oldalán (egyenlő bizonyult a fenti részecskék bisectors) és két szög (első egyenlő a állapotban, az utóbbi a függőleges), úgy, hogy a visszamaradó részecskék bisectors is egyenlő egymással, és így maguk teljesen felezővonal. QED.

Probléma 6. Bizonyítsuk be, hogy az a szegmens hosszát összekötő közepén, a két oldalán egy háromszög egyenlő fele egy harmadik fél.

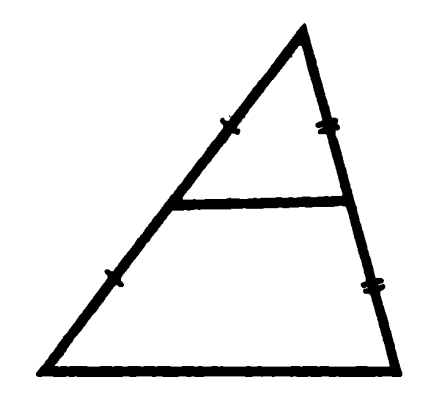
Neat oldalán az úgynevezett „bázisok” keresztbe - „lágyék”

A bizonyíték: az oldalán a kis és nagy háromszög a képen kezelik 1, 2, továbbá van egy közös szögben, így ezek hasonlóak a második funkció a hasonlósági faktor 1, 2, és ezért a bázis egyaránt 1, és 2. Az QED.

Probléma 7. Bizonyítsuk be, hogy az átlós paralelogramma osztja két egyenlő háromszög.

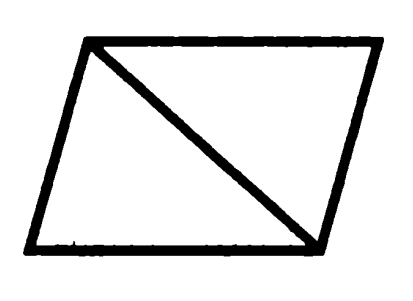
Paralelogramma átlós több, talán nincs is hozzá

Bizonyítás: szemközti oldalán egy paralelogramma egyenlő, az átlós gyakori mellékhatása ilyen háromszög, így azok egyenlő három oldalról. QED.

Probléma 8. Bizonyítsuk be, hogy a medián, derékszögű háromszög átfogója felhívjuk felével egyenlő az átfogó.

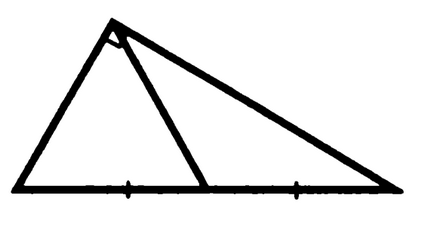
Más szóval, a medián végzett a csúcsa a derékszög

Bizonyítás: Ha bárhol egy adott derékszögű háromszög leírni a kör, a beírható kör egyenes szög a háromszög kerül bemutatásra egy félkör, így a átfogója a kör átmérője, és a fele az átfogónak és adott nekünk a problémát a medián - sugarak, így azok mind egyformák. QED.

Feladat 9. Igazoljuk, hogy a szegmensek érintőjének a kerülete egy pont, egyenlő.

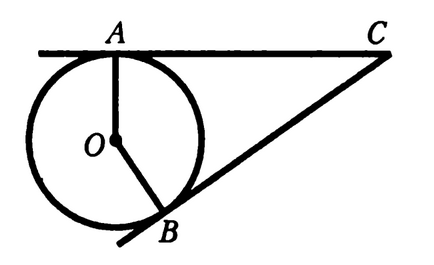
Kiegészítő építési: csatlakoztassa a C pont-pont O (mentálisan)

A bizonyíték: a B és A szögben vonalak (sugara egy kör lefolytatott ponton oszcillációs merőleges a tangens), ez azt jelenti, a derékszögű háromszögek AOC, és BOC jelentése mentén átfogója (a teljes ezeket a képzeletbeli érintkezési oldallal OC) és a láb (a körön OB = OA), és így AC = CB. QED.

Feladat 10. Bizonyítsuk be, hogy az átmérő közepén áthaladó kör húrja merőleges rá.

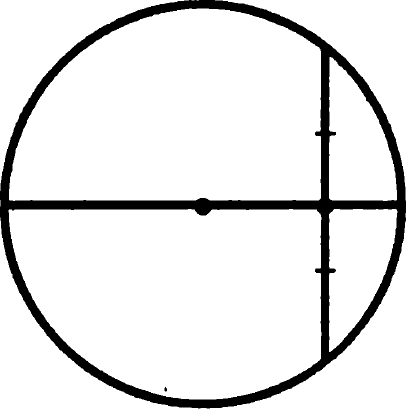
Az összekötő vonal két pont az ábrán a medián a háromszög, amely figyelembe vesszük

Bizonyítás: Az egyenlő szárú háromszögben metszéspontjai a húrt a kör és a a kör közepén ábrázolt a medián magas lesz, és így az átmérő, amely önmagában a magassága merőleges a húrt. QED.

Feladat 11. Mutassuk meg, hogy ha a két kör közös akkord, a vonal közepén áthaladó e körök merőlegesen az adott akkord.

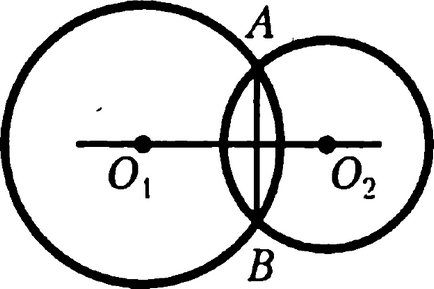
Értelmi csatlakoztassa össze minden jelölt pontok az ábrán, a metszéspont az úgynevezett vízszintes és függőleges irányban H

A bizonyíték: a háromszögek és O1AO2 O1BO2 van három oldalról, tehát, ∠HO2A = ∠HO2B. Ezután Háromszögmódszert HAO2 és HBO2 egyenlő mindkét oldalon, és a köztük lévő szög, majd ∠AHO2 = ∠BHO2. és kiszámítjuk a két egyenlő szög adhat 180 0 csak akkor, ha azok mindegyike a 90 0. QED.

Feladat 12. Mutassuk meg, hogy ha egy kör írható, négyszög, az összeg a hossza szemközti oldalai egyenlők.

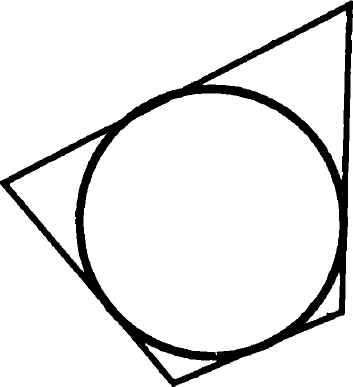
Érintőnégyszög. Nevezzük ABCD. Legyen M, E, X és L - pont kapcsolatot

Probléma 13. Bizonyítsuk be, hogy ha egy négyszög lehet leírni, mint egy kör, akkor az összege a szemközti szögek egyenlők.

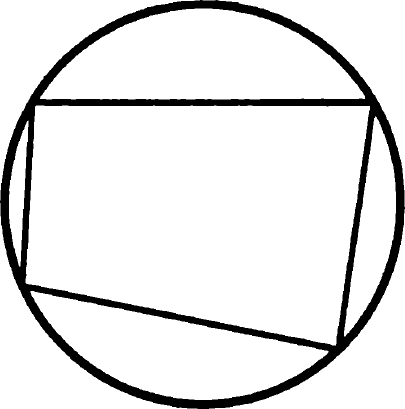
Igazolást a tétel a kerületi szög összege szemközti szögek egy négyszög 180 0. óta együtt támaszkodni egy teljes kör, ami méri a 360 fokos 0. QED.

Probléma 14. Bizonyítsuk be, hogy ha néhány, a trapéz lehet leírni, mint egy kör, a egyenlő szárú trapéz.

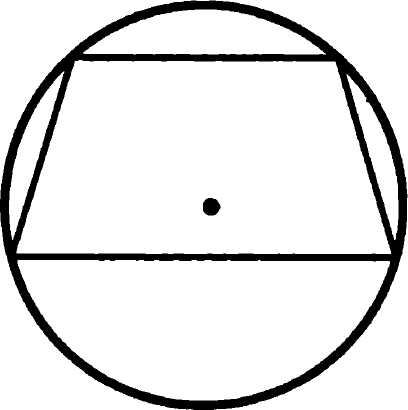
Egyenlő szárú trapéz írt egy kört

Bizonyítás: A összege átellenes szögek egy négyszög feltüntetik egy kör, α + β = 180 0 (lásd a feladat 13.), A szögek összege az oldalán a trapéz is megegyezik α + γ = 180 0 (ezeket a szögeket oldalú a párhuzamos bázisok és a szelő oldalsó oldalán) összehasonlítjuk ezeket képletek azt kapjuk, hogy β = γ. vagyis a szögek az alapja egy trapéz egyenlő, és ez tényleg egyenlő szárú. QED.

Cél 15. A ABCD négyzet pont K és E - a közepén az AB és az AD, ill. Bizonyítsuk be, hogy merőleges legyen KD CE.

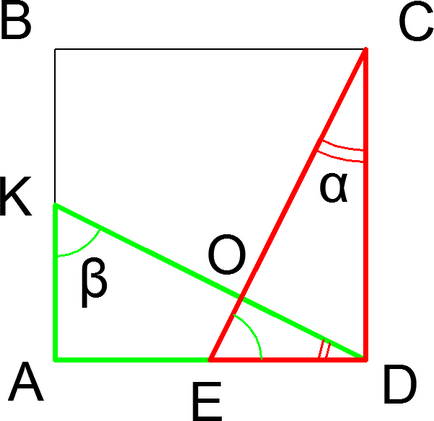
Kép a feladathoz

Bizonyítás. Derékszögű háromszögek AKD és ECD két Catete, így egyenlő és minden elemük. enged

Az összeg háromszög szögei egyenlők, ha például, van AKD háromszög, és így a háromszög EOD van, ami van, és ezért mi bizonyítja merőleges KD és CE.

Bizonyított geometriai tények fontosak, tudásukat lesz nagy segítség megoldásában bonyolultabb problémákat geometria, elsősorban a munkahelyek C4 lehetőség EGE a matematikában. Az itt bemutatott magyarázza az összehasonlító oldatok, amelyeket meg kell tenni a vizsgát, persze, nem. Ezek csak mutató, mely segítségével az olvasó képes lesz megoldást találni a saját.

Mindenesetre, a képességét, hogy megoldja a problémákat, a geometriában elengedhetetlen feltétele a magas pontszámot a vizsgát, és GIA matematika, amely garantálja belépést számos rangos egyetemeken. Sok szerencsét a felkészülés a KF és a USE, tehetséges tanár és sok sikert a vizsgán! A tutor Szergej V. geometria.