Hogyan lehet megtalálni az alapja a trapéz

Beállítása egy ilyen négyszög, trapéz, mint meg kell határozni legalább három oldalról. Ezért például, hogy lehetséges legyen a probléma, abban az állapotban, hogy meghatározza a hossza az átlók trapéz. és az egyik oldalon vektorok.

Ábra feltételei a probléma az 1. ábrán látható Ebben az esetben azt kell feltételezni, hogy a fenti Trapezoid - egy négyszög AVCD, ahol az előre meghatározott hossza átlók AC és BD, és egy oldalsó felület AB, képviseli a vektor egy (ax, ay). A kapott adatok forrása lehetővé teszi számunkra, hogy két osnovaniyatrapetsii (alsó és felső). Egy konkrét példában az alacsonyabb bázis AD lesz található először.

Tekintsük ABD háromszög. A hossza az AB oldal egyenlő nagyságának. Legyen | a | = sqrt ((ax) ^ 2 + (Ay) ^ 2) = a, majd cosf = ax / sqrt (((ax) ^ 2 + (Ay) ^ 2) az az irány, koszinusz egy let megadott. p van egy átlós hossza a BD és az AD kívánt hosszúságú s. Ezután, a koszinusz, P ^ 2 = a ^ 2 + x ^ 2-2axcosf. Vagy 2-2axcosf x ^ + (a ^ 2-p ^ 2) = 0 .

Solutions A másodfokú egyenlet: X1 = (2acosf + sqrt (4 (a ^ 2) ((cosf) ^ 2) -4 (a ^ 2-p ^ 2))) / 2 = acosf + sqrt ((a ^ 2) ((cosf) ^ 2) - (a ^ 2-p ^ 2)) == a * ax | sqrt (((ax) ^ 2 + (Ay) ^ 2) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + Ay ^ 2)) - a ^ 2 + p ^ 2) = AD.

Ahhoz, hogy megtalálja a nap felső alap (a hossza megoldásokat találjanak is kijelölt X) használjuk modulusa | a | = a, és egy második átlós BD = q és a koszinusza az ABC szög, ami egyértelműen egyenlő (p-p).

Következő tartják az ABC háromszög, amely, mint korábban, a koszinusz tétel alá, és ott van a következő megoldás. Tekintettel arra, hogy cos (n, p) = - cosf alapján a megoldást az AD, tudjuk írni a következő képlet helyett p aq: BC = - egy * ax | sqrt (((ax) ^ 2 + (Ay) ^ 2 ) + sqrt ((((a) ^ 2) (ax ^ 2)) / (ax ^ 2 + Ay ^ 2)) - a ^ 2 + q ^ 2).

Ez az egyenlet egy másodfokú és rendre két gyökerei. Így ebben az esetben az, hogy csak azokat a gyökereket, amelyek pozitív érték, mivel a hossza nem lehet negatív.

PrimerPust trapéz ABCD oldalsó AB által adott vektor egy (1, sqrt3), p = 4, q = 6. Keresse osnovaniyatrapetsii .Reshenie. Algoritmusok segítségével fentiekben levezetett felírható: | a | = a = 2, cosf = 1/2. AD = 1/2 + sqrt (4/4 -4 + 16) = 1/2 + sqrt (13) = (sqrt (13) +1) /2.BC=-1/2+sqrt (-3 + 36 ) = (sqrt (33) -1) / 2.

Trapéz tekinthető négyszög, amelynek két oldala párhuzamos, a másik kettő nem. A magasság a trapéz nevezzük szegmens húzott merőleges két párhuzamos csík között. Attól függően, hogy a nyers adatok alapján lehet kiszámítani a különböző módon.

• Knowledge oldalán bázisok középvonalas trapéz, valamint, adott esetben, a terület és / vagy kerület.

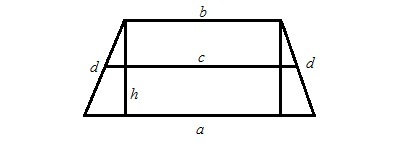
Az egyik módja annak, hogy kiszámítja a területet a trapéz a termék a magasság és a középső sor. Tegyük fel, hogy van egy egyenlő szárú trapéz. Ezután a magassága egyenlő szárú trapéz bázisokkal a és b, az S felület és a kerület P a következőképpen számítjuk ki:

h = 2 x S / (P-2 x d). (Lásd. 1. ábra)

Ha csak egy ismert területe a trapéz és bázis, a magassága számítási képlet származhatnak a terület a trapéz képletű S = 1 / 2h X (a + b):

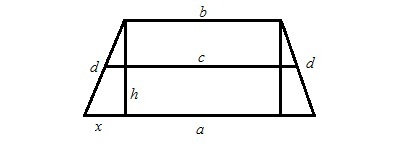
Tegyük fel, van egy trapéz ugyanazokkal az adatokkal, mint az 1. ábra 2. Draw magassága, megkapjuk egy téglalap, amelynek két kisebb oldala a derékszögű háromszög. Jelöljük kisebb hengerek x. Azt találtuk, hogy elosztjuk a hosszának különbsége a nagyobb és a kisebb bázisok. Ezután, a tétel Pitagorasz tér a magassága azonos a négyzetének összege a átfogója és a láb d x. Fogadás a gyökere ennek az összegnek és kap a magassága h. (Ábra. 2)

A matematikai alak négy szög hívják a trapéz, ha a pár ellentétes oldalain párhuzamos és a másik pár - nem. Párhuzamos oldalai úgynevezett osnovaniyamitrapetsii. A másik két - oldalán. Egy téglalap alakú trapéz egyik sarok az oldalán - line.

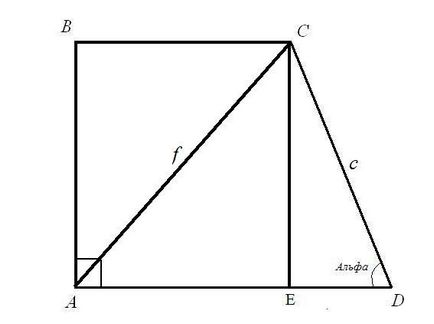
Feladat 1.Locate BC alap és az AD téglalap trapéz. ha tudjuk, hogy a hossza az AC átló = f; oldalhosszúságú CD = c és szöget annak ADC = α.Reshenie: Vegyünk például egy derékszögű háromszög CED. Ismert átfogója c közötti szög az átfogó és a lábszár EDC. Get hosszúságú oldalakkal CE és ED: szög, amelyet a képlet CE = CD * sin (ADC); ED = CD-cos (ADC). Tehát: CE = c * sinα; ED = c * cosa.

Vegyünk egy derékszögű háromszög ACE. Átfogója AC és CE lábát tudja, hogy az oldalsó AE szabály által a derékszögű háromszög: a négyzetének összege a lábak egyenlő a tér a átfogója. Tehát: AE (2) = AC (2) - CE (2) = f (2) - c * sinα. Számoljuk ki a négyzetgyöke a jobb oldali. Megtalálta a felső alapja a téglalap, trapéz.

AD bázis hossza a hosszúságok összegét két vonal szegmensek AE és ED. AE = négyzetgyök (f (2) - c * sinα); ED = c * cosa) .Itak: AD = négyzetgyök (f (2) - c * sinα) + c * cosα.Vy talált négyszögletes alsó alap egy trapéz.

Feladat 2.Locate BC alap és az AD téglalap trapéz. ha tudjuk, hogy a hossza a BD átlója = f; oldalhosszúságú CD = c és szöget annak ADC = α.Reshenie: Vegyünk például egy derékszögű háromszög CED. Keresse meg a hossza az oldalán CE és ED: CE = CD * sin (ADC) = c * sinα; ED = CD-cos (ADC) = c * cosa.

Vegyünk egy téglalap ABCE. A tulajdonság a téglalap AB = CE = c * sinα.Rassmotrite derékszögű háromszög ABD. Az ingatlan a derékszögű háromszög négyzet átfogójának egyenlő a négyzetének összege a másik két oldala van. Ezért, AD (2) = BD (2) - AB (2) = f (2) - c * sinα.Vy talált alacsonyabb bázis a trapéz téglalap AD = négyzetgyök (f (2) - c * sinα).

A téglalap szabály BC = AE = AD - ED = négyzetgyökét (f (2) - c * sinα) - * cosα.Vy találtak a felső alap a négyszögletes trapéz.

Kisebb bázis a trapéz párhuzamos egyik oldala, amelynek minimális hossza. Számolja ez az érték több módon, segítségével néhány adatot.

Ha tudja, hogy a hossza a két - egy nagy alapja a trapéz és a középső vonal - kiszámításához használt legkisebb alapja a trapéz tulajdon. Eszerint, a középső sor azonos fele a trapéz alapja. Ebben az esetben a legkisebb alap egyenlő a különbség kétszerese a hossza a középvonal és a hossza a nagy bázisa a szám.

Ha az ilyen paraméter ismert trapéz, mint a területen, magasság, hosszúság a nagy bázis, a számítás a legkisebb bázis az ábra, hogy vezesse a alapján területe a trapéz formula. Ebben az esetben, a végeredmény kivonásával kapott a különbség kétszerese a privát terület és a magassága olyan paraméter, mint a hossza a nagy trapéz alapja.

A hossza a legkisebb oldalán egy téglalap alakú trapéz úgy számítjuk ki, egy másik módszerrel. Ez a paraméter egyenlő a termék a hossza a második oldalon, és a szinusz a hegyesszöget bezáró accumbensben. Azokban az esetekben, amikor a szög nem ismert, a rövidebbik oldalán hasonlítható a magassága a trapéz és kiszámítása Pitagorasz-tétel segítségével. A legkisebb oldalán egy téglalap alakú trapéz megtalálják a koszinusz-tétel: s² = a² + b²-2ab * cosa; ahol a, b, c jelenti az oldalán a háromszög; α az oldalai közötti szög a és b.