Hogyan lehet megoldani a rendszer egyenletek két ismeretlen

addíciós módszerrel.
két egyenlet kell írni szigorúan egymás alá:

Ezután hajtsa mindegyik kifejezés egyenletek, illetve az előjelek figyelembevételével:

2 + (- 9X) = - 7x, -5u 5Y + 0 = 61 + (- 40) = 21. Jellemzően az egyik összegeket tartalmazó ismeretlen érték nulla lesz.
Írja az egyenletet a kapott tagok:

-7x + 0 = 21.
Find ismeretlen: -7H = 21, h = 21 (- 7) = - 3.
Helyettesítő már talált érték bármelyik egyenletek és kezdő, hogy megkapja a második ismeretlen, oldja meg a lineáris egyenlet:

2-5u = 61, 2 (-3) = -5u 61 -6-5u = 61 + 61 = -5u 6 -5u = 67, y = -13.4.
A válasz az egyenletrendszert: x = -3, y = -13.4.

helyettesítő módszer.
Az egyik egyenletet kell kifejezni bármelyik szükséges tagok:

x + 5Y = 61, X = 61 + 5Y.
Helyettesíteni az egyenletet kapjuk a második a szám helyett az „X” (ebben az esetben):

lineáris egyenlet, hogy megtalálják a szám „y”:

-549 + 45U + 4y = -7, 45U + 4Y = 549-7, 49u = 542, y = 542: 49, u≈11.
A véletlenszerűen kiválasztott (ki) helyett az egyenlet helyezze már talált „y” szám a második 11 és kiszámítja az ismeretlen:

X = 61 * 11 + 5, X = 61 + 55 = 116 x.
Adott választ az egyenletrendszert: x = 116, y = 11.

Grafikus módon.
Van hogy gyakorlati pont koordinátái, amelyek átfedik egyenes matematikailag rendszerben rögzített egyenletek. Szükséges felhívni a diagramok közvetlenül is külön-külön azonos koordináta rendszerben. Az általános nézet az egyenlet egyszerű: - y = kx + b. Megépíteni a sorban, ez elegendő ahhoz, hogy megtalálja a koordinátáit a két pontot, s, x véletlenszerűen választják.
Adott egy rendszer: 2x - y = 4

-3H + y = 1.
Épült, közvetlenül az első egyenletben, az egyszerűség kedvéért meg kell írni: y = 2x-4. Gyere fel (világosabb) értékek X, hogy ebben az esetben ez az egyenlet megoldása, azt, hogy megtalálják y. Kapott két pontot, amelyek irányítják az építőipar. (Lásd ábra.)
0 X 1

y -4 -2
Épült, közvetlenül a második egyenletet használva: y = -3H + 1.
Csak építeni a vonalat. (Lásd ábra.)

y 1 -5
Keresse meg a koordinátáit metszéspontja két egyenes épített a chart (ha a vonalak nem metszik egymást, akkor a rendszer nem megoldás - ez történik).

Hogy megoldja a rendszer egyenletek két változó általánosan használják a következő módszerek: grafikus eljárással, a helyettesítési és a módszer mellett. Tartózkodási az első a fenti kiviteli alakokban.

Tekintsük a szekvenciája megoldások a rendszer, amely a lineáris egyenletek formájában: a1x + b1y = C1 és a2x + b2y = c2. Ahol x és y - ismeretlen változó, és b, c - a szabad feltételeket. Ha ezt a módszert alkalmazzuk minden megoldás rendszer közvetlen koordináta pontok mindegyikének megfelelő egyenletet. Kezdjük azzal, hogy minden esetben kifejezni egy változót a másik felett. Ezután állítsa az x változó többé értékeket. Elég, ha kettő. Helyettesítsük be az egyenletet, és találja y. Build a referenciakeret, jelölje meg a pontot kapott rajta, és fut egyenesen rajtuk keresztül. Hasonló számításokat kell végezni, más részei a rendszernek.

A lényeg vagy metszéspontja a grafikonok épített és lesz megoldás ennek egyenletrendszer.

A rendszernek van egy egyedülálló megoldás, ha épített vonalak metszik egymást, és egy közös pont. Ez ellentmond, ha a grafika nem párhuzamosak egymással. És végtelen sok megoldás, ha a közvetlen egyesítés egymással.

Ez a módszer akkor tekinthető nagyon világos. A fő hátrány az, hogy a számított ismeretlenek megközelítő értékek. Egy pontosabb eredményt kap az úgynevezett algebrai módszerek.

Bármilyen megoldás a rendszer érdemes megnézni. Ehhez helyettesítse a változók kapott értékeket. Azt is megtalálja a megoldást több szempontból is. Ha az oldat a rendszer van, jól választ kapjon ugyanaz.

Gyakran vannak olyan egyenleteket, amelyekben egy vagy több feltétel nem ismert. Hogy oldja meg ezt az egyenletet, meg kell emlékezni, és kész a megadott számok a konkrét intézkedéseket.

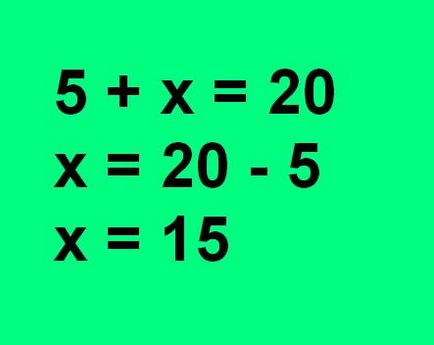
Megoldás rendszerek - egy meglehetősen bonyolult szakasza az iskolai tananyag. A valóságban azonban, van néhány egyszerű algoritmust, amely lehetővé teszi, hogy ezt gyorsan. Egyikük - a megoldás hozzátéve módszer rendszereket.

A lineáris egyenletrendszer egy kombinációja két vagy több egyenlet, amelyek mindegyike két vagy több ismeretlen. Két fő megoldási módozatok rendszerek lineáris egyenletek, amelyeket az iskolai tantervbe. Egyikük az úgynevezett helyettesítési módszer, a másik - a módszert alkalmazunk.

A szabványos formája a rendszer két egyenlet

A szabványos formában az első egyenlet a forma A1 * x + b1 * y = c1, a második egyenlet a2 * x + b2 * y = c2, és így tovább. Például, abban az esetben egy kétrészes rendszer mindkét fenti egyenletek a1, a2, b1, b2, c1, c2 - numerikus együtthatók, bemutatva a specifikus egyenletek. Az viszont, x és y ismeretlen, amelynek értékeit kell meghatározni. Kifizeti a szükséges értékek mindkét egyenlet egyszerre igaz egyenlőséget.

A döntés azt jelenti, hogy felül rendszer

Annak érdekében, hogy megoldja a felül azt a rendszert, amely az, hogy megtaláljuk a az x és y, ami viszont őket valódi egyenlőség, szükség van arra, hogy egy néhány egyszerű lépésben. Az első az, hogy megtérít minden az egyenletek úgy, hogy a numerikus együtthatók a változó x vagy y mindkét egyenletben ugyanaz nagyságú, de különböznek jel.

Tegyük fel például, hogy van egy rendszer, amely a két egyenlet. Ezek közül az első a következő alakú 2x + 4y = 8, a második forma 6x + 2y = 6. Az egyik feladata a második kiviteli alak a szorzás együtthatója a 2. egyenlet, amely elvezeti -12x-4Y = -12 szem előtt. A helyes választás az együttható egyik legfontosabb feladat a folyamat, amely során a folyamat a megoldás, mert ez határozza meg az egész jövőjét megtalálni az ismeretlen eljárást.

Most már el kell végezni a két új egyenletrendszerek. Nyilvánvaló, hogy a kölcsönös pusztítás változók azonos értékű, de ellenkező előjellel az együtthatók vezet formájában -10x = -4. Ezt követően meg kell oldani egy egyszerű egyenlet, amelyből egyértelműen kiderül, hogy x = 0,4.

Az utolsó lépés a folyamatban a megoldás a helyettesítése a talált érték az egyik változók bármely eredeti egyenletek a rendszerben rendelkezésre álló. Például, helyettesítésével x = 0,4, az első egyenletben, megkaphatjuk expressziós 2 * 0,4 + 4y = 8, ahol y = 1,8. Ennek megfelelően az X = 0,4, és y = 1,8 gyökerei vannak elrendezve a példában rendszerben.

Annak érdekében, hogy megbizonyosodjon arról, hogy a gyökerek talált igaz, hasznos, hogy csekk helyett a mért értékeket a második egyenletben a rendszer. Például, ebben az esetben, az egyenlőség kapunk formájában 0,4 * 6 + 1,8 * 2 = 6, ami igaz.