Hogyan lehet bizonyítani, hogy a háromszög hegyesszögű 1

Vannak kísérletek, amelynek kimenetelét nem lehet leírni egy véges terek elemi események. Ezekben az esetekben néha hasznos fogalom geometriai valószínűség.

Tegyük fel, hogy az a tér W elemi események néhány kísérlet része a valós vonal vagy sík részének vagy részletének a tér, amelynek véges mérték m (W). By sokaságát értjük olyan intézkedés, a hossz, terület, illetve a térfogatnak. Egy véletlen esemény egy részhalmaza W. teret, amely véges mérték m (W). Majd a valószínűsége P (A) az A esemény határozza meg (geometriai valószínűség).

Ezt a módszert számításához használt valószínűségi, amikor a feltételek a kísérlet a valószínűsége egy elemi esemény (tekintve a tér W) A halmaz arányos intézkedés A halmaz, és nem függ a helyét a térben W. Ebben az esetben azt mondjuk, hogy a véletlenszerűen kiválasztott ponton egyenletesen oszlik el térben W.

D példa a sugarú kör véletlenszerűen elhelyezett három pontot az A, B és C a valószínűsége, hogy hegyesszögű ABC háromszög.

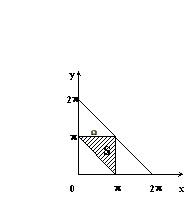
Mi hosszát méri a készülék köríveinek pontok közötti olyan irányban, hogy ha mozog a kerület azon a ponton, majd egy B pont, mint egy B pont - pont C. Legyen x - ív hossza AB keresztül y - Sun ívhossz. Ezután a különféle kimenetelek a kísérlet vizsgált lehet hasonlítani szempontjából HOY síkban x és y koordinátákat kielégítik az alábbi egyenlőtlenségeket, azaz.

Ha S esemény - hegyesszögű ABC háromszög, majd a.

Nyilvánvaló, hogy a területen a régió W egyenlő 2 p 2. és a terület S a területen. Lásd. Ábra. 1. Ennek a valószínűsége. D