Hogyan állapítható meg, az ív sugara vagy körcikk, és megtalálja a központban - Dr. törmelék

Az első módszer a meghatározására az ív sugara vagy körszegmens

Kezdetben úgy néz ki:

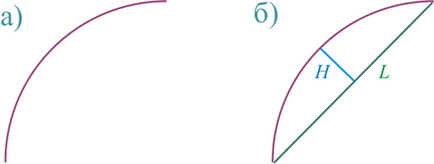
Ábra 463,1. a) ív áll, b) meghatározzuk a szegmens húrhossz és magassága.

Így, ha van egy ív, akkor csatlakoztassa a végeit és kap ívhossza L. közepén a húrt tudjuk felhívni a vonal merőleges a húrt, és így kapjuk a magassága a szegmens H. Most, ismerve a húr hossza és a magassága a szegmens, akkor először meghatározzák a központi szöget α, azaz közötti szög a sugarak levonni az elején és végén a szegmens (az ábrán 463,1 ábrán nem látható), majd a kör sugara.

A megoldás egy ilyen probléma tartották néhány részlet a cikkben: „Számítási ívelt híd”, ezért itt csak azt mutatja, az alapvető képlet:

Mint látható, a szempontból a matematika nem jelent problémát a meghatározása a körön nem. Ez a módszer lehetővé teszi, hogy meghatározza az értékét a sugara az ív esetleges pontossággal. Ez a fő előnye ennek a módszernek.

Beszéljünk a hiányosságokat.

A probléma ezzel a módszerrel még csak nem is az a tény, hogy úgy emlékszik a képletek az iskolai geometria természetesen sikeresen elfelejtett sok évvel ezelőtt - emlékeztet a képlet - van internet. De arctg számológép funkció, arcsin, és így tovább. nincs minden felhasználó számára. Bár ez a probléma is sikeresen megoldja az interneten, de nem szabad elfelejteni, hogy úgy döntünk, elég alkalmazásokhoz. Ie nem mindig szükséges, hogy meghatározzuk a kör sugarát pontossággal 0,0001 mm, pontossága 1 mm lehet egészen elfogadható.

Ezen túlmenően, annak érdekében, hogy megtalálják a közepén a kör, akkor ki kell terjeszteni a magassága a szegmensben, és tegye ezt a vonalat egyenlő távolság a sugár. Mivel a gyakorlatban van dolgunk nem ideális mérőműszerek, ehhez hozzá kell adni a lehetséges hiba a jelölésben, kiderül, hogy minél alacsonyabb a magassága a szegmens hosszához képest a húrt, annál is jön a hiba meghatározásakor az ív közepén.

Ismét nem szabad elfelejteni, hogy nem tartjuk ideális eset, azaz a Erre azért van szükség, azonnal a görbe az ív. Sőt, ez lehet egy görbe által leírt meglehetősen bonyolult matematikai összefüggés. Azért így talált és a sugara a kör középpontjának nem feltétlenül esik egybe a tényleges központja.

Ebben a tekintetben, szeretnék javasolni egy másik meghatározó módszer kör sugarát, ami önmagában gyakran, mert ily módon meghatározzák a kör sugara sokkal gyorsabb és könnyebb, de a pontosság sokkal kevésbé.

A második módszer a meghatározására az ív sugara (a módszer az egymást követő közelítő értékek)

Tehát továbbra is vizsgálja a jelenlegi helyzetet.

Mivel még mindig meg kell találni a közepén a kör, akkor meg kell kezdeni a pontok megfelelő elején és végén az ív, évente legalább két ív tetszőleges sugarú. Át a kereszteződés ezen ívek lesz közvetlen, és hol van a központja a kívánt kört.

Most arra van szükség, hogy csatlakozzanak a közepén metszi a körív húrja. Azonban, ha tartunk ezek a pontok nem ugyanazon ív, és két, ez egyenes haladna át a kereszteződés ilyen ívek, majd keresse meg a közepén a húrt nem szükséges.

Nos, akkor ez egyszerű: mérje meg a távolságot a kereszteződés az ív kezdete előtt (vagy vége) az ív vonatkozóan, akkor a távolság a kereszteződés az íveket a megfelelő pontot a szegmens magasság.

Ha a távolság a kereszteződés az íveket, hogy az elején vagy végén az ív megfontolás alatt nagyobb, mint a távolság a metszéspontja az ívek a megfelelő pontban a magassága a szegmens, az azt jelenti, hogy az az ív közepén vizsgált alatt van a húzott egyenes vonaltól közepén keresztül a kereszteződés az ív és az akkord. Ha kevesebb is - köteles fölött az ív közepén a vonalon.

Ezen az alapon a vonalon által elfogadott következő pont, feltehetően megfelelő ív közepén, és ez tette ugyanazokat a méréseket. Ezután veszi a következő pont, és ismételje meg a mérést. Minden új mérési pont a különbség kisebb lesz.

Ez minden. Annak ellenére, hogy ilyen hosszadalmas és trükkös leírás meghatározására az ív sugara ily módon pontossággal 1 mm elég 1-2 perc.

Elméletileg ez így néz ki:

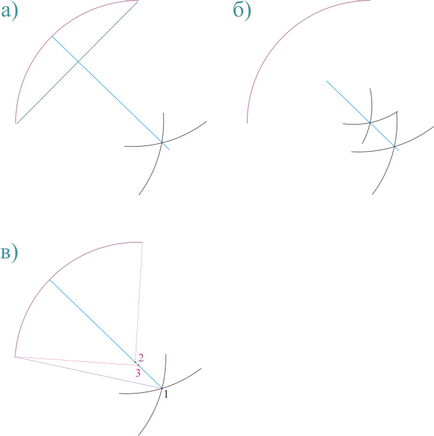
Ábra 463,2. Meghatározás ív középponti követő közel.

A gyakorlatban azonban, valahogy így:

Photo 463,1. Particionálás előformagyártó bonyolult alakzatokat különböző sugárral.

Csak akkor Hozzáteszem, hogy néha szükség van, hogy megtalálja, és felhívni néhány sugarak, mert a fotó annyira, és összekeverjük.

Csatlakozó száma Yandex Wallet 410012390761783

Vagy a térképen 5106 2110 0462 8702 A címzett Sergei Gutov

Ukrajna - hrivnya kártyaszám (Privatbank) 5168 7423 0569 0962 A címzett Gutov Szergej Mihajlovics

Mindenesetre, egy erszényt WebMoney: R158114101090