Fekvő keresztben szögek párhuzamos vonalak egyenlő

Van egy tétel, hogy a vonalak párhuzamosak, ha a kereszteződésekben a keresztmetszet fekvő keresztben szögek egyenlők. Mivel itt - egyenlő szögek a kereszt hazugság a vágás, ennek eredményeként - a párhuzamos.

Van egy inverz tétel fekvő keresztben metsző szögek egyenlők, amikor áthalad a párhuzamos vonalak. Ebben az esetben, ez adott - a párhuzamos vonalak, eredmény - az egyenlőség fekvő keresztben metsző szögben.

Az ellenkezője tétel „túlzott”? Nem tudom csak mondani, hogy az egyetlen párhuzamos vonal feküdt keresztben metsző szögek egyenlők? De lehet, hogy ezek a szögek egyenlő, és néhány nem párhuzamos vonalak. Azaz, a párhuzamos, akkor világos, hogy vannak, de vannak más vonalak is, egyenlő szögek. Az ellenkezője tétel kizárja ezt a lehetőséget.

Tétel bizonyítása inverz csökkenti a következőket.

Feltételezzük az ellenkezőjét, azaz a. E. hogy az adatok párhuzamos vonalak fekvő keresztben metsző szögek nem egyenlő. Tegyük fel, hogy a párhuzamos vonalak a és b, amely áthalad a keresztirányú C. Tegyük fel, hogy a kereszt fekvő szögek 1 és 2 nem egyenlő: ∠1 ≠ ∠2.

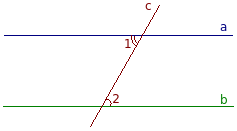
Miután a szelő metszéspont az egyik párhuzamos vonalak (b) felhívni egy egyenes vonalat d úgy, hogy egyenlő szemzugszög fekvő keresztben 1 3: ∠1 = ∠3.

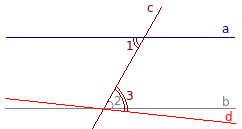
Közvetlen tétel kimondja, hogy ha hazudik keresztben metsző szögek egyenlők, akkor a vonalak párhuzamosak. Ennélfogva, a vonalak a és d párhuzamosak: a || d.

Kiderült, hogy egy közös pont (amelyek átfedik egyenes vonalak b, c, d) elvégzett két párhuzamos vonal (B és D), amelyek párhuzamosak a vonal egy. Mindazonáltal, a korábban bizonyított tétel, ez nem lehet: egy ponton nem feküdt egy egyenes vonal, akkor dolgozzon csak egy párhuzamos vonalat.

Ezért a feltételezés, hogy ∠1 ≠ ∠2, ez nem igaz. Ezért ∠1 = ∠2. Nincs más egyenes, amely áthalad egy adott pont, amely megadja az egyenlő szögek a keresztmetszete, kivéve az egyetlen párhuzamos.