Ábrázolása kvadratikus függvények az algoritmus és példák
legfontosabb nbsp> nbsp Wiki-bemutató nbsp> nbsp Matematika nbsp> nbsp9 osztály nbsp> nbspPostroenie grafikon kvadratikus függvények: az algoritmus és példák
A másodfokú függvény olyan függvény a formában:
y = a * (x ^ 2) + b * x + c,
ahol a - együtthatója a legmagasabb fokú ismeretlen x,
b - együttható az ismeretlen x,
és - egy szabad tag.
A grafikon a másodfokú függvény görbe az úgynevezett a parabola. Az általános formája a parabola az alábbiakban kerül bemutatásra.
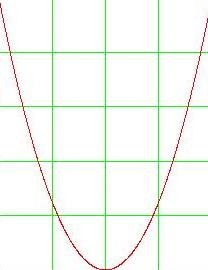
1. ábra Az általános nézet az parabola.
Számos különböző módszerek cselszövés másodfokú függvényt. Nézzük meg az alap és a leggyakoribb ezek közül.
Egy algoritmust építése a grafikont a másodfokú függvény az y = a * (x ^ 2) + b * x + c
1. Szerkesszünk egy koordinátarendszerben említett intervallumon, és jelentkezzen koordinátatengelyeken.
2. Határozza meg az irányt a parabola ágait (felfelé vagy lefelé).
Ehhez nézd meg a jele az együttható a. Ha egy plusz - az ágak felfelé irányított, ha negatív - az ágak alján.
3. Határozzuk meg az x koordináta csúcsa a parabola.
Ehhez használja a következő képletet Hvershiny = -B / 2 * a.
4. Határozza meg a koordinátákat a csúcsa a parabola.
Erre a szubsztituált egyenletbe Uvershiny = a * (x ^ 2) + b * x + c x helyett találtak az előző lépésben értéket Hvershiny.
5. Alkalmazza a kapott pontot a menetrend, és folytatni azt a szimmetria tengelye párhuzamos az y tengellyel koordináta.
6. Keresse meg a metszéspont a grafikont, az x tengely.
Ez megköveteli, hogy megoldja a másodfokú egyenlet egy * (x ^ 2) + b * x + c = 0 az egyik ismert módszerekkel. Ha az egyenlet nincsenek valós gyökei, akkor a függvény grafikonját metszi az x-tengelyen.
7. Keresse meg a koordinátáit a metszéspont a grafikon az y tengelyen.
Az ezt az értéket szubsztituált egyenletbe X = 0, és az A értékét y. Megjegyezzük, ezt, és szimmetrikus pont a grafikonon.
8. Keresse meg a koordinátáit egy tetszőleges pont (x, y)
Ehhez válasszon egy tetszőleges értéket az x koordináta, és helyettesíti azt a mi egyenletben. Kapunk az érték ezen a ponton. Alkalmazza egy pont a grafikonon. Megemlítendők a grafikonon a tükörképe a pont (x, y).
9. Csatlakoztassa a kapott pontok a grafikonon sima vonal, és továbbra grafikon végpontok végéig a koordináta tengely. Bejelentkezés a menetrend, vagy a léggömb, vagy ha a tér lehetővé teszi, valamint a grafikon is.
Példa ábrázolási
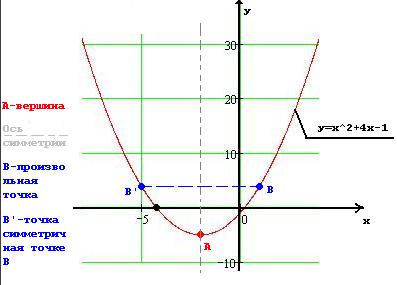
Példaként, megkonstruálunk egy grafikon a másodfokú függvény által adott y = x ^ 2 + 4 * X-1
1. Rajzolj koordinátatengelyeken, aláírja és figyelmét az egység intervallum.
2. Az értékek a együtthatók a = 1, b = 4, c = -1. Mivel a = 1, amely nagyobb, mint nulla parabola ága felfelé irányuljon.
3. Határozzuk meg az x koordináta a parabola csúcsa Hvershiny = -B / 2 * A = 4/2 * 1 = -2.
4. Határozza meg a koordinátákat a csúcsa a parabola
Uvershiny = a * (x ^ 2) + b * x + c = 1 * ((- 2) ^ 2) + 4 * (- 2) - 1 = -5.
5. Jegyezze fel és tartsa a szimmetria tengelye.
6. Keresse meg a tér a grafikon metszéspontja az x tengely. Megoldása másodfokú egyenlet x ^ 2 + 4 * X-1 = 0.
x1 = -2-√3 x2 = -2 + √3. Megjegyezzük, a kapott értékeket a diagramon.
7. Keresse meg a menetrend metszéspontja az y tengelyen.
X = 0; y = -1
8. Válasszon egy tetszőleges pont B. Legyen ez az a koordináta az x = 1.
Akkor Y = (1) ^ 2 + 4 * (1) -1 = 4.
9. Elhelyezés a kapott pontok és jel ütemtervet.
Az eredmény az lesz a menetrend.