A legegyszerűbb elsőrendű differenciálegyenlet, példák, oldatok
Ebben a cikkben fogunk foglalkozni a megoldás a legegyszerűbb elsőrendű differenciálegyenletek, amelyek nem tartalmazzák az ismeretlen függvény y. Az ilyen differenciálegyenletek, amelyek vagy már megoldott a származék, vagy meg lehet oldani, tekintettel a származékot.
Az általános megoldás a differenciális egyenletek formájában, egy előre meghatározott intervallumban X megtalálható integrálásával mindkét oldalán ennek az egyenletnek. Kapjuk. Ha viszont a tulajdonságait határozatlan integrál. majd megkapjuk a kívánt, teljes megoldást y = f (x) + C, ahol F (x) - egyike a primitívek f (x) intervallumban X. és C - egy tetszőleges konstans.
Megjegyezzük, hogy az X tartomány nem jelzett sok problémát. Ebben az esetben azt jelenti, hogy a megoldást kell keresni minden x. és amelyben az ismeretlen függvény y. és az eredeti egyenlet van értelme.
Ha szeretné megtalálni egy adott megoldást a differenciálegyenlet, amely megfelel a kezdeti feltétel y (x0) = y0. miután megállapította, a teljes szerves y = f (x) + C továbbra is szükség van, hogy kiszámítja a konstans értékét C = C0. A kezdeti feltétel. Azaz, az állandó C = C0 a következő egyenletből meghatározzuk F (x0) + C = y0. és a kívánt különösen differenciálegyenlet formájában y = f (x) + C0. Vegyünk egy példát.
Keresse az általános megoldás a differenciálegyenlet, helyességét ellenőrizni az eredményt. Keressen egy partikuláris megoldása ennek az egyenletnek felel a kezdeti feltételt.
Integrálása a kezdeti differenciálegyenlet, megkapjuk. Ez az integrál hogy az eljárás integrálás:

Így - az általános megoldás a differenciálegyenlet.
Annak ellenőrzésére, az eredmény pontossága a csekket. Ehhez a kapott oldathoz, hogy helyettesítse az eredeti egyenletet:
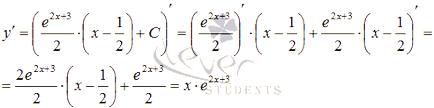
Ezért, amikor a kezdeti egyenlet válik identitás, így az általános megoldás a differenciálegyenlet talált helyesen.
Meg kell jegyezni, hogy a talált megoldás az általános megoldás a differenciálegyenlet minden érvényes értékek az érvelés x.
Továbbra is, hogy meghatározzák a konkrét megoldást a ODE a kezdeti feltétel. Más szóval, meg kell találni a C értéke állandók melyik lesz igaz egyenlőséget.
Ezért, hogy ebben az esetben a C = 2 az általános megoldás a TAC kapjunk egy adott oldatot egy differenciálegyenlet, amely megfelel egy előre meghatározott kezdeti állapot.
Rendes differenciálegyenlet megoldható az a származék, elosztjuk mindkét oldalán az f (x). Egy ilyen átalakulás egyenértékű lenne, ha f (x) nem egyenlő nullával bármely x-intervallumban integráció a differenciálegyenlet X.
Lehetnek olyan esetek, amikor mindkét kapcsolja nullára egyes értékek az érvelés x ∈ X f (x) és g (x). Az ilyen értékek az x az általános megoldás a differenciálegyenlet minden funkciója y. meghatározott őket.
Ha az argumentum valamely x ∈ X értékek a feltételeket, akkor a ODE nincs megoldásokat.
A pihenési intervallum X X általános megoldása a differenciálegyenlet határozzuk meg a konvertált egyenlet. Nézzük az alábbi példát.
Keresse az általános megoldás közönséges differenciálegyenlet.
Mivel tudjuk, hogy az alapvető tulajdonságait az elemi függvények, hogy a természetes alapú logaritmus függvény definiált a pozitív értékek a érv azonban doménje a függvény y = ln (x + 3) az az időköz x> -3. Következésképpen, a kezdeti differenciálegyenlet is jelentene az x> -3. Ezeken értékek az érvelés expressziós x + 3 nem lesz nulla, tehát, meg lehet oldani a származékot TAC, elosztjuk mindkét oldalról x + 3 lesz.
Most, hogy integrálja a kapott differenciálegyenletek megoldott a származék :. A vevő ezt a szerves használjuk a módszert társítása jele eltérés. . Így - az általános megoldás a differenciálegyenlet az x> -3.
Találd meg az összes megoldást a differenciálegyenlet.
A differenciálegyenlet értelme az összes valós x. Ha feltételezzük, hogy x ≠ 0. átalakíthatjuk formájában ODE. Amikor x = 0 a kiindulási egyenlet válik egy identitást bármilyen funkciót meghatározott x = 0. Tehát, ha x = 0 megoldása a differenciálegyenlet minden funkciója y. meghatározva nulla érv.
Mi integrálja a differenciál egyenletet:
- differenciálegyenlet, ha x = 0 megoldása a differenciálegyenlet minden függvény erre a értéke az érv.
Keresse az általános megoldás közönséges differenciálegyenlet.
sinx eltűnik az. Ahhoz, hogy ezek az érvek cosx ≠ 0. Ezért, az értéke a kezdeti differenciálegyenlet nincs megoldása. Ebben az esetben tudjuk osztani mindkét oldalról sinx. Megkapjuk az ODE megoldódott-származék. Integrálni :. Így - az általános megoldás egy differenciálegyenlet.
- Èl'sgol'ts LE Differenciálegyenletek és variációszámítás.