A kötet a prizma
Mi a kötet a prizma és hogyan találják meg
Prism térfogata - a termék a terület annak bázis és a magasságot.
Tudjuk azonban, hogy az alap a prizma lehet háromszög, négyzet, vagy bármely más poliéder.
Ezért, hogy megtalálják a térfogata prizmák, akkor csak meg kell számítani a területen a bázis a prizma, majd ezen a területen szorozni a magassága.
Azaz, ha az alap a háromszög prizma, akkor először meg kell találni az eszközöket, a háromszög területe. Ha az alap prizma egy négyzet vagy más sokszög, akkor először meg kell nézni azt jelenti területe a téren, vagy más sokszög.
Tartsuk szem előtt, hogy a magassága a prizma merőleges, felhívjuk az alapja a prizmát.
Mi a prizma
És most idézzük a meghatározása a prizma.
Prism - egy sokszög, két felülete (bázis), amelynek vannak párhuzamos síkokban, és minden él párhuzamos a külső ezeknek a felületeknek.
Egyszerűen fogalmazva, ez:
Prism - bármilyen geometriai alakú, ami két bázis egyenlő egymással, és sík felületekből.
Cím a prizma függ a bázis formájában. Ha a bázis egy háromszög prizma, úgy, hogy a háromszög alakú prizma hívást. Sokoldalú prizma nevezzük mértani alakzat, az alapja, amely egy poliéder. Szintén prizma - egyfajta henger.
Milyen típusú prizma
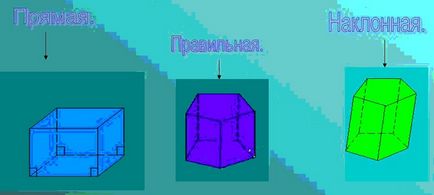
Ha megnézzük a fenti képen azt látjuk, hogy a prizma egyenes, jobbra és ferde.
1. Mi az úgynevezett prizma megfelelő?
2. Miért hívják ezt?
3. Mi a neve annak a prizma, amelynek bázisok szabályos sokszögek?
4. Mi a magassága a szám?
5. Hogyan nevezzük prizma, amelynek szélei nem merőleges?
6. Adja meg a meghatározását egy háromszög alakú prizma.
7. Lehet hasáb prizma?
8. Mi a geometriai alak úgynevezett semiregular sokszög?
Mik az elemek egy prizma
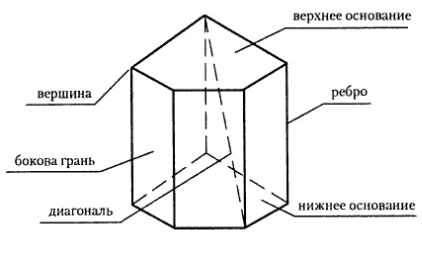
A prizma áll elemek, például az alsó és felső bázis, oldallapjai, élek és csúcsok.
• Mindkét hasáb bázis és hazugság párhuzamos síkban egymással.
• Az oldalsó felületei a piramis - ez egy paralelogramma.
• Az oldalsó felületén a piramis az összege az oldalsó arcok.
• Gyakori mellékhatások oldallapja, nem más, mint az oldalsó széleit a szám.
• A magassága a piramis egy szegmens összekötő a talaj síkja és a rá merőleges.
tulajdonságok prizma
A geometriai alak, mint egy prizma, számos tulajdonságait. Vessünk egy közelebbi pillantást ezeket a tulajdonságokat:
• Először is, a bázisok a prizma nevezzük szabályos sokszögek;
• Másodszor, az oldalsó felületek a prizma kerülnek bemutatásra formájában paralelogramma;
• Harmadszor, ezt a geometriai forma bordák párhuzamosak és egyenlő;
• Negyedszer, a teljes felülete a prizma:
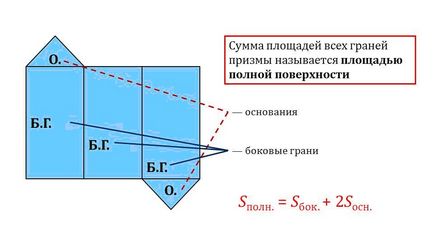
Most úgy tétel, amely formula, amely a számított oldalsó felülete a bizonyíték.

Érdekes tények a prizma
Gondolt már arra, az ilyen érdekes tény, hogy a prizma lehet nem csak a geometriai test, hanem más tárgyak körül bennünket. Még a közönséges hópehely hőmérséklettől függően lehet alakítani jeges prizma, figyelembe formájában hatszögeknél.
De kalcitkristályok van egy ilyen egyedi jelenség, hogy szétesik darabokra, és alakjuk mezőbe. És a legmeglepőbb, hogy mi volna a kis alkatrészek nem zúzott kalcitkristályok, az eredmény mindig ugyanaz, ők pedig egy Tiddly mezőbe.
Kiderül, hogy egy prizma tett szert népszerűségre nem csak a matematikában, bemutatva annak geometriai test, hanem a művészetek, mert ez az alapja a festmények által létrehozott nagy művészek, mint Picasso, Braque, Griess és mások.