A kör sugara, átmérő, pi, szektor, tangens
Kerület - plane pontok helye, amelynek távolsága a középponttól a kerülete egyenlő.
Sugár. távolságra a központtól, a kör a határ.
Átmérőjű. a legnagyobb távolság egy kerületi másikig. Az átmérő kétszerese a sugár.
Határoló (kerülete). kerületének határán.


Kerület $ = \ pi \ alkalommal $ átmérő
Doug. egy görbe vonal, amely része a kör.
Arc fokban mérik vagy radiánban. Például: 90 °, vagy $ \ frac $ - negyed kör, 180 vagy $ \ pi $ - fele a kör.
A összessége ívek 360 °
Az akkord. egy összekötő szakasz két pontot a kör.
Ágazatban. mint egy darab süteményt (ék).
A kör érintője: az egyenes merőleges a sugara, és amelynek csak egy közös pontja a okurzhnostyu.
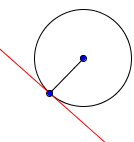

Kerület $ = \ pi \ cdot \ text = 2 \ cdot \ pi \ cdot \ text $
kör nagysága $ = \ pi \ cdot $ 2 tartomány
A sugár jelöljük r. a d átmérő. P, mint a kerület és a terület mindkét S.
$ P = \ pi \ cdot d = 2 \ cdot \ pi \ cdot R $
$ S = \ pi \ cdot r ^ 2 $
Area egy körcikk, K. (központi szög $ \ theta $ sugár és az $ r $).
Ha a szög $ \ theta $ fokban, majd a területen = $ \ frac \ pi r ^ 2 $
Ha a szög $ \ theta $ radiánban, majd a területen, akkor a terület = $ \ frac r ^ 2 $
Ha az ív hossza $ \ theta $ minősítési vagy radiánban, az értéke a központi szöget $ \ theta $ (fok vagy radián).
Ha tudja, hogy a hossza az ív (. A hüvelyk, yard, láb, hüvelyk, méter) megtalálja az érték a megfelelő központi szög ($ \ theta $) a következő képlet segítségével:
kerületi szög
Kerületi szög egy szöget vertex a kerülete, és az oldalaik, amelyek tartalmazzák a húrt a kör.
Az ábrán, APB szög kerületi szög.
Az érték a kerületi szög fele az ív, amelyekre hivatkozik.
például:
$ \ Widehat = 84 ^ \ circ $
$ \ Angle APB = \ frac = 42 ^ \ circ $
1. eset: a két secants metszik belső kerülete.
Amikor két secants metszi a körön belül, a szög értéke, amelyet két-szer kisebb az érték az íveket, amelyeken alapulnak. Ábra ív ív AB és CD 60 ° és 50 °, míg szögek az 1. és 2. egyenlő $ \ frac (60 ^ \ CIRC + 50 ^ \ circ) = 55 ^ \ circ $
2. eset: Két metsző metszi a körön kívül.
Néha secants metszik a körön kívül. Amikor ez történik, a méret a kapott szög egyenlő közötti különbség felével az ívek, amelyeken alapulnak.
$ \ ABC szög = \ frac (x - y) $
Az ábra AB ív = 80 °, és az ív CD = 30 °.
$ \ ABC szög = \ frac (80 - 30) = \ frac \ cdot 50 = 25 ^ \ circ $
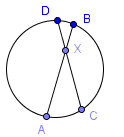

Ha két akkordok metszi belső kerületén, a fentiek szerint, majd a:
$ AX \ cdot XB = CX \ cdot XD $