A háromszög és a kör
Köré írt kör a háromszög nevezzük. ha az összes, a háromszög csúcsait található a kör.
A közepe egyenlő távolságra az összes csúcsot, akkor ott kell lennie a metszéspontja a függőleges felezővonal a háromszög oldalai.
Következésképpen bármilyen háromszög lehet leírni, mint egy kör, hiszen a közép-merőlegesek az oldalról metszik egy ponton.
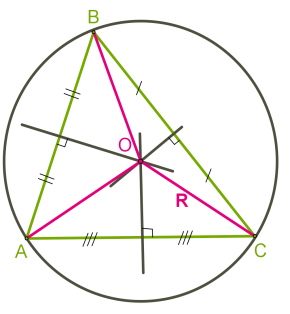
A hegyesszögű háromszög az a kör középpontja a háromszög.
Egy másik helyzet négyszögletes és tompa háromszög.
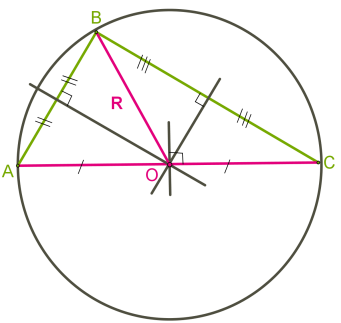
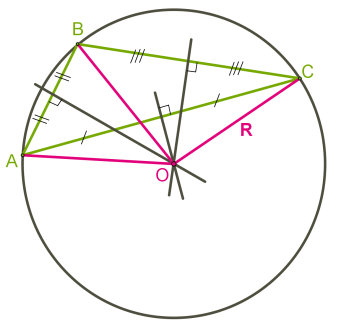
A beírható kör háromszög
A beírható kör háromszög nevezzük. ha minden oldalán a háromszög érintik a kört.
A közepe egyenlő távolságra minden oldalról, hogy van, kell, hogy legyen a metszéspontja a bisectors a háromszög.
Következésképpen olyan háromszög kör írható, mint a felezővonal a háromszög metszik egy ponton.
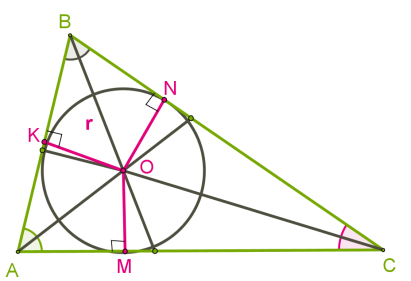
Mivel a felezővonal egy háromszög szögei mindig metszik a háromszögön belül, a központ minden háromszög beírt kör a háromszög.
Az egyenlő oldalú háromszögben egybeesnek szögfelező, medián és magassága, vagyis ezek a szegmensek is midperpendiculars. Ez azt jelenti, hogy a központok a körülírt és beírt körének ugyanaz.
A sugara a körülírt kör
R = 3 február h. Ezért, R = 3 márciusban.
A sugara a beírt kör
r = 1 március h. ahol \ (h \) - a magassága a háromszög.
Ha az oldalán a háromszög kap \ (a \), majd h = 2 márciusban.
Ezért, R = a június 3
A sugara a körülírt kör
R = 1 február c. ahol \ (c \) - átfogója.
A sugara a beírt kör
r = S δ p. ahol \ (p \) - semiperimeter.
A sugara a körülírt kör
R = a ⋅ b ⋅ c 4 ⋅ S δ
R = a 2 sin α. ahol α - szög ellenkező oldalon \ (a \).
ha S δ = abc 4 R. akkor R = abc 4 S δ; ha S δ = p ⋅ r. akkor R = S δ p