A hallgatók felkészítése a vizsgát a képzési központ felbontású (referencia Matematika - geometria

• Céljai érdekében
• másodfokú trinomiális
• Egyenletek és egyenlőtlenségek
  modulokkal
• Számtani és mértani sorozat
• koordináta módszerrel
  a gépen
• Ábrák egy koordináta által meghatározott sík egyenlőtlenségek
• Megoldás algebrai egyenletek
• A megoldás a racionális egyenlőtlenségek
• A döntés irracionális egyenlőtlenségek
• Megoldás az exponenciális egyenletek
• Megoldás bemutató egyenlőtlenségek
• Megoldás logaritmikus egyenletek
• Megoldás logaritmikus egyenlőtlenségek
• az egyenletrendszert
• Megoldás trigonometrikus egyenletek
• Trigonometry vizsga
  matematika
• Fokú racionális kitevő

HIVATALOS oktatási anyagok

Sphere feltüntetik egy prizma. A tulajdonságait egyenes hasáb, gömb leírt mintegy

1. meghatározása egy gömb felirat olvasható prizma nevezzük gömb érinti a síkok minden prizma oldalait. ahol az érintkezési pontok fekszenek arcok a prizma (ábra. 1).

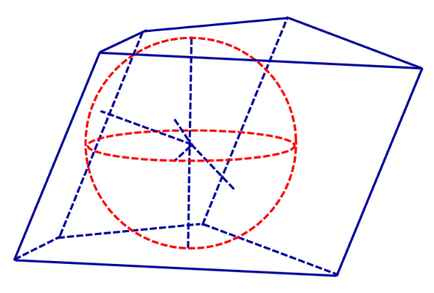
Definíció 2. Ha a gömb felirat olvasható prizma, prizma nevezzük gömb le kb.

Így, ha egy prizma van leírva a körét, sík felületeivel a prizma síkok érintő a gömb.

Jóváhagyása. Ha egyenes prizma feliratos sugarú gömb R. a prizma magassága 2R, és a prizma bázis lehet írt kör sugara R.

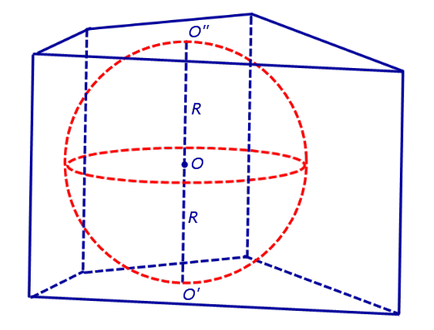
Jelölje O középpontjában a beírt gömb és szimbólumok O „és O„-. Sphere érintési pont a síkban a prizma bázisok Megjegyezzük, hogy a prizma alap síkjával párhuzamos sugarak OO”. És OO" tartott körét az érintési pont a síkban a prizma bázisok és ezért síkjára merőlegesen a prizma bázis. Ezért, a közvetlen O'O „merőleges síkok a bázisok a prizma, a központ a beírt gömb O a középpontját a szegmens O'O” és prizma magassága megegyezik a hossza a szegmens O'O „, és egyenlő a 2R.

Keresztül az O pont merőleges síkban egyenes O'O”. És azt mutatják, hogy minden területen a tapintási pont az oldalsó felületei prizma hazugság ebben a síkban. Ehhez jelöljük körét az érintkezési pont bármely aspektusa a prizmát az L betű, és bizonyítani, hogy a vonal OL egyenesre merőleges O'O „(3.).

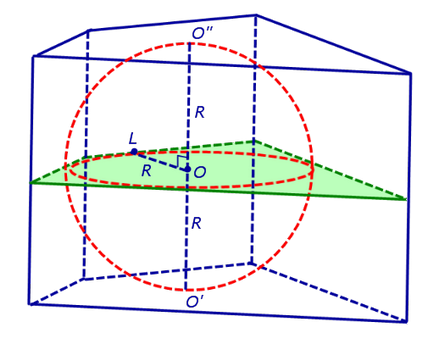
Sőt, OL sugara. tartott az érintési pont a gömb oldalfelületén a prizma síkjára merőleges ez az arc. és ezért merőleges bármely egyenes feküdt ez az arc, és beleértve, OL merőleges a pereme a prizma.

Figyelembe vett prizma egy egyenes hasáb, így az oldalsó élei mentén merőleges síkok a bázisok. Közvetlen O'O „is merőleges a síkok a bázisok és ezért párhuzamos oldalsó szélei a prizma. Ezért arra lehet következtetni, hogy a vonal merőleges vonal OL O'O”, és ezáltal olyan síkban fekszik merőleges egyenes O'O „és ponton áthaladó O.

A keresztmetszete a prizma és a sík a gömb ezekben feltüntetett merőleges vonal O'O „, és áthalad az O pont, egy sokszög. Prizmák egyenlő alapon egy kört az ezekben feltüntetett R sugarú (ábra. 3).

Következmény. Mindenesetre kocka lehet feliratos szférában.

A kötet aránya egy gömb és a kocka leírt körüli gömb határoló léggömb

Probléma 1. Keresse az arány a kötet egy gömb és kocka körülhatárolt egy gömb, amely korlátozza a ballon.

Határozat. Ha a gömb sugara R feltüntetik egy kocka, a kocka éle egyenlő 2R (ábra. 4).

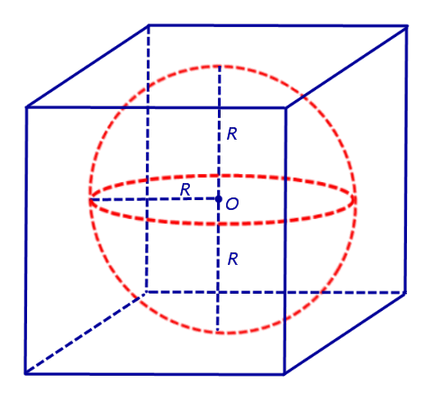
és a térfogatot kocka 2R kiszámítása a képlet:

Következmény 1. Az arány a kötet egy gömb térfogatának egy szabályos háromszög prizma le a gömb alakú befoglaló el egyenlő

2. Következmény aránya kötet egy gömb térfogatának egy szabályos négyszögletes hasáb le a gömb alakú befoglaló el egyenlő

Megjegyzés. Ahogy látható, egybeesik a képlet n = 4 képlet a térfogat arány a válasz (2. tétel) (1).

3. Következmény Az arány a labdát a kötet egy szabályos hatszög hasáb le a gömb alakú befoglaló el egyenlő

Azt is megismerkedhetnek a tanárok kifejlesztett egy képzési központ „rezolvens” tananyagok, hogy felkészüljenek a vizsgára matematikából.

A diákok, akik szeretnék jól felkészülni, és átmennek a vizsgán, vagy OGE (DPA) matematika, fizika vagy magyar nyelven a magas pontszámot, a képzési központ „rezolvens” tartja