A felület a kúp - a képlet, egy példa a számítási

Most itt van: Matematika> Geometry> A felülete egy kúp

Let α - síkon az S pont - pont, hogy nem hazudik ebben a síkban. Tekintsünk egy tetszőleges síkban sugarú kör R. A Csatlakoztassa tetszőleges pontja ennek a körnek szegmens S AS pont. Ha pont lenne leírni a körön R. szegmensek AS kitölti valamilyen szervezetben. Ez a szerv az úgynevezett kúpos.

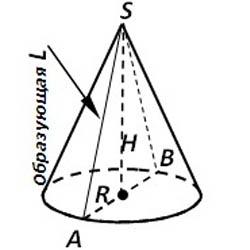
A határ a kúp egy R sugarú kör és az oldalsó felületének a kúp.
Oldalfelülete leírja az AS szegmens. ha az A pont a kört ír le.
Point S a a kúp csúcsánál. AS több szegmensből. összekötő a vertex a kerülete a bázist irányítsák konusa.Esli merőleges csökkent ponttól S. egybeesik a központ a bázis, a kúp mondják pryamym.Ochen gyakran azt mondta, hogy a közvetlen a kúp által alkotott forgás tengelye körül egy téglalap alakú háromszög, amelynek a lábát.
Ezen az ábrán, egy egyenes kúp fordult forgása által egy téglalap alakú háromszög AOS körül a lábát SO. majd azt mondják

SO láb a kúp magassága;
Átfogója AS generátor kúp;
Leg AO - a sugara a kúp.

A terület a palástfelület a kúp révén sugara és útmutató

Adott egy kúp R sugarú és alkotó L
AS = L, AO = R

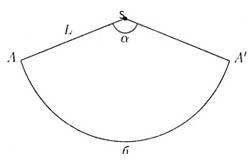
Vágjuk az alkotó mentén a kúp L és telepítéséhez oldalsó felületén.
Az eredmény egy ívháromszögének ASA`. ahol AS = L, A`S = L.
Arc egy AA` hosszúkás kúpos alaprész sugarú kör R. Következésképpen, az ív hossza egyenlő 2πR AA`
A terület a palástfelület olyan körszegmens egyenlő a terület sugarán R.
Ha a szög α - intézkedés radiális szög, akkor:
ahol α = ∠
Ahhoz, hogy megtalálja a szög ∠ Képletkifejezések ívhosszúság hogy subtends egy adott szög:
De másfelől:
Mi egyenlőségjelet tesznek a jobb oldalon. Van:
Express α:
Behelyettesítve ezt a kifejezést a terület az ágazatban:
Következésképpen, az oldalsó felülete a kúp egyenlő a termék számának π sugara a kúp és a generátor.
Formula oldalsó felülete a kúp lesz a következő formában:

Példa terület számítása kúpos, ha ismerjük a sugara, és a vezetőelem
Find a terület az oldalsó felületének a kúpon egy 3 cm sugarú, kialakítva egy útmutató 7 cm
A feladat szerint L = 5 cm, R = 3 cm
Formula kúp:

Behelyettesítve a képlet értékét a feltételeket, a probléma, van:

A terület a palástfelület a kúp révén sugarát és magasságát

Nagyon gyakran problémákat számítani a területet az oldalsó felületén kúp kúp magassága ismert, ahelyett, hogy irányítja azt.
Mivel a kúp sor, az AOS háromszög - szögletes, ahol AO és OS - a lábak és az AS -gipotenuza. A Pitagorasz-tétel, megkapjuk:
Így:
de
majd:
Behelyettesítve ezt a kifejezést az oldalán felülete a kúp:
Az oldalsó felülete a kúp egyenlő a számot a kúp sugár és a négyzetgyöke az összege az sugara és magassága a kúp négyzetek

Példa terület számítása kúpos ha tudjuk sugarát és magasságát.
Find a terület az oldalsó felületének a kúpon egy sugara 1 cm, magassága pedig 5 cm
A feladat szerint H = 5 cm, R = 1 cm
Formula kúp:

Behelyettesítve a képlet értékét a feltételeket, a probléma, van:

A teljes felülete a kúp

A teljes felülete a kúp - az összeg a terület a palástfelület és a tér alapja a kúp:

kúp bázis egy sugarú kör R. Ez területe egyenlő a termék számának π és a négyzetével sugara:
Palástfelületén van képlettel számítottuk ki: vagy
Ekkor a teljes felület a kúp egyenlő:
vagy
Így a teljes felülete a kúp egyenlő a számot a kúp sugara és az összeg a sugár és az útmutató.
A képlet a következő:
Teljes felülete a kúp egyenlő a termék számának π sugara kúp és egy összege négyzetgyökének négyzetösszeg a sugár és magassága a kúp és a kúp sugara.
A képlet a következő: