6. osztály aránya, matematika, ismétlés

Az egyenlő két arány hívják arányban.

Példa arányok. 1 2. 3 = 16. 4. Ez egyenlő két arány: 12: 3 = 4 és 16: 4 = 4. Követő: tizenkét úgy utal, hogy a három. mint tizenhat utal négy. Itt, 12. és 4 tag -Rendkívül arányok, és a 3. és 16. - a középső arányához viszonyítva.

A fő tulajdonsága arányban.

A termék a szélsőséges tagjai aránya a termék átlagos tagja.

Mert arányok a. b = c. d vagy a / b = c / d van írva, mint az alapvető tulajdonságát: a · d = b · c.

A mi aránya = 12 3 16 4 alapvető tulajdonság felírható: = 12 · 4 16 · 3. Kiderült, a valódi egyenlőség: 48 = 48.

Ahhoz, hogy megtalálja egy ismeretlen tagja a szélsőséges képarány, szükség van a termék átlagos arányait a tagok osztva jól ismert tagja a szélsőséges.

Példák. Keressen egy ismeretlen tagja a szélsőséges arányokat.

x = (20 · 2): 5 - meg kell szorozni az átlagos tagok (20 és 2) és oszd el az utolsó ismert tagja (az 5. számú);

X = 40. 5. - a termék az átlag tagja (40) van osztva egy jól ismert tagja a szélsőséges (5);

X = 8. megkapjuk a kívánt arányban a szélsőséges tagja.

Sokkal kényelmesebb felvenni találni egy ismeretlen részét a tag által a közös frakcióban. Ez úgy van, ahogy van írva mi tekinthető egy példa:

Keresek extrém tagja aránya (x) egyenlő a termék a középső tagok (20 és 2) osztva az ismert szélsőséges elem (5).

Cut frakciót 5 (osztva 5, és a számláló és a nevező a frakció). Mi vagyunk a megállapítás az x értékét.

Ha elfelejtette hogyan kell csökkenteni a közös frakciókat, majd ismételje meg a témát: „5.4.2. Példák a frakciók csökkentés "

Mégis az ilyen példák jelenlétében egy ismeretlen tagja a szélsőséges arányok.

Ahhoz, hogy megtalálja egy ismeretlen részét a középső kifejezés, meg kell dolgozni szélső tagja arányban osztva ismert átlagos tagja.

Példák. Keressen egy ismeretlen részét annak a közép-távon.

5) 9. 14. X = 3. száma 3 - átlagos tagja e, ismert arányban a 9. és 14. - szélsőséges arányokat.

X = (9 × 14) 3 - szaporodnak szélsőségek arányban, és az eredményt osztva az átlagos tagja ismert arányban

A megoldás ebben a példában lehet írni másképpen:

Keresek átlagos tagja aránya (x) egyenlő a termék szélső tagja (9 és 14) osztva az ismert átlagos tagja (3).

Vágott 3. frakció (osztás 3, és a számláló és a nevező a frakció). Mi vagyunk a megállapítás az x értékét.

Ha elfelejtette hogyan kell csökkenteni a közös frakciókat, majd ismételje meg a témát: „5.4.2. Példák a frakciók csökkentés "

Mégis az ilyen példák jelenlétében egy ismeretlen hányada a középső kifejezés.

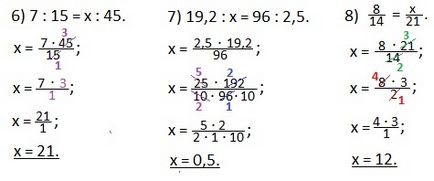
Oldal 1 1 1